
【題目】將線段![]() 繞點
繞點![]() 逆時針旋轉角度
逆時針旋轉角度![]() 得到線段
得到線段![]() ,連接
,連接![]() 得
得![]() ,又將線段
,又將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得線段
得線段![]() (如圖①).
(如圖①).
![]() 求
求![]() 的大小(結果用含
的大小(結果用含![]() 的式子表示);
的式子表示);
![]() 又將線段
又將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得線段
得線段![]() ,連接
,連接![]() (如圖②)求
(如圖②)求![]() ;
;
![]() 連接
連接![]() 、
、![]() ,試探究當
,試探究當![]() 為何值時,
為何值時,![]() .
.

【答案】(1)![]() ;(2)
;(2)![]() ; (3) 當
; (3) 當![]() 為
為![]() 時,
時,![]() .
.
【解析】
(1)由于線段AB繞點A逆時針旋轉角度α(0°<α<60°)得到線段AC,根據旋轉的性質得AB=AC,∠BAC=α,利用等腰三角形的性質和三角形內角和定理得到![]() 再由線段BC繞點B逆時針旋轉60°得線段BD,根據旋轉的性質得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD進行計算;
再由線段BC繞點B逆時針旋轉60°得線段BD,根據旋轉的性質得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD進行計算;
(2)由線段AB繞點B順時針旋轉60°得線段BE,根據旋轉的性質得AB=AE,∠BAE=60°,則AC=AE,∠CAE=60°-α,利用等腰三角形的性質和三角形內角和得到![]() 然后利用∠BCE=∠ACB+∠ACE計算得到∠BCE=150°;
然后利用∠BCE=∠ACB+∠ACE計算得到∠BCE=150°;
(3)由線段BC繞點B逆時針旋轉60°得線段BD,根據旋轉的性質得BC=BD,∠CBD=60°,則可判斷△BCD為等腰直角三角形,則∠BCD=60°,CD=BC,
所以∠DCE=∠BCE-∠BCD=90°,加上∠DEC=45°,于是△DEC為等腰直角三角形,則CE=CD,所以CB=CE,然后利用“SSS”證明△ABC≌△AEC,得到∠BAC=∠EAC,所以![]()
![]() ∵線段
∵線段![]() 繞點
繞點![]() 逆時針旋轉角度
逆時針旋轉角度![]() 得到線段
得到線段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得線段
得線段![]() ,
,
∴![]() ,
,
∴![]() ;
;

![]() ∵線段
∵線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得線段
得線段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;![]() 如圖②,
如圖②,
∵線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得線段
得線段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
當![]() 為
為![]() 時,
時,![]() .
.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,M為BC上一點,F是AM的中點,EF⊥AM,垂足為F,交AD的延長線于點E,交DC于點N.

(1)求證:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2002年國際數學家大會在北京召開,大會選用了趙爽弦圖作為會標的中心圖案.如圖,由四個全等的直角三角形與一個小正方形拼成一個大正方形.如果大正方形的面積是25,直角三角形較長的直角邊長是a,較短的直角邊長是b,且(a+b)2的值為49,那么小正方形的面積是( )

A.2B.0.5C.13D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點.現從點
的中點.現從點![]() 觀察線段
觀察線段![]() ,當長度為
,當長度為![]() 的線段
的線段![]() (圖中的黑粗線)以每秒
(圖中的黑粗線)以每秒![]() 個單位長的速度沿線段
個單位長的速度沿線段![]() 從左向右運動時,
從左向右運動時,![]() 將阻擋部分觀察視線,在
將阻擋部分觀察視線,在![]() 區域內形成盲區.設
區域內形成盲區.設![]() 的左端點從
的左端點從![]() 點開始,運動時間為
點開始,運動時間為![]() 秒
秒![]() .設
.設![]() 區域內的盲區面積為
區域內的盲區面積為![]() (平方單位).
(平方單位).

![]() 求
求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
![]() 請簡單概括
請簡單概括![]() 隨
隨![]() 的變化而變化的情況.
的變化而變化的情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師出示了小黑板上的題后(如圖),小華說:過點(3,0);小彬說:過點(4,3);小明說:a=1;小穎說:拋物線被x軸截得的線段長為2.你認為四人的說法中,正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線 ![]() 的函數表達式為
的函數表達式為![]() ,且直線
,且直線![]() 與x軸交于點D.直線
與x軸交于點D.直線![]() 與x軸交于點A,且經過點B(4,1),直線
與x軸交于點A,且經過點B(4,1),直線![]() 與
與![]() 交于點
交于點![]() .
.

(1)求點D和點C的坐標;
(2)求直線![]() 的函數表達式;
的函數表達式;
(3)利用函數圖象寫出關于x,y的二元一次方程組![]() 的解.
的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,線段AB、CD相交于點O,連接AD、CB,我們把形如圖1的圖形稱之為“8字形”.如圖2,在圖1的條件下,∠DAB和∠BCD的平分線AP和CP相交于點P,并且與CD、AB分別相交于M、N.試解答下列問題:
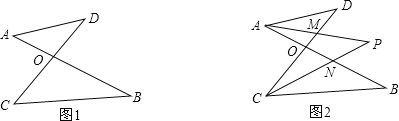
(1)在圖1中,請直接寫出∠A、∠B、∠C、∠D之間的數量關系: ;
(2)仔細觀察,在圖2中“8字形”的個數: 個;
(3)圖2中,當∠D=40°,∠B=30°度時,求∠P的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個長為4cm,寬為3cm的長方形木板在桌面上做無滑動的翻滾(順時針方向),木板點A位置的變化為A→Al→A2,其中第二次翻滾被面上一小木塊擋住,使木板與桌面成30°的角,則點A滾到A2位置時共走過的路徑長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com