
【題目】隨著“互聯網+”時代的到來,傳統的教學模式也在悄然發生著改變.某出國培訓機構緊跟潮流,對培訓課程采取了線上線下同步銷售的策路,為了讓客戶更理性的選擇,該機構推出了甲、乙兩個課程體驗包:甲課程體驗包價值660元含3節線上課程和2節線下課;乙課程體驗包價值990元含2節線上課程和5節線下課程.
(1)分別求出該機構每節課的線上價格和線下價格;
(2)該機構其中一個銷售團隊上個月的銷售業績為:線上課程成交900節,線下課成交1000節.為回饋客戶,本月該機構針對線上、線下每節課程的價格均作出了調整:每節課線上價格比上個月的價格下調a%,線下價格比上個月的價格下調![]() a%,到本月底統計發現,該銷售團隊線上成交的課程數比上個月增加了
a%,到本月底統計發現,該銷售團隊線上成交的課程數比上個月增加了![]() a%,線下成交的課程數上升到1080節,最終團隊的月銷售總額線上比線下少了54000元,求a的值.
a%,線下成交的課程數上升到1080節,最終團隊的月銷售總額線上比線下少了54000元,求a的值.
 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 是一次函數
是一次函數![]() 的圖象和反比例函數
的圖象和反比例函數![]() 的圖象的兩個交點.
的圖象的兩個交點.
![]() 求直線
求直線![]() 與
與![]() 軸的交點
軸的交點![]() 的坐標及
的坐標及![]() 的面積;
的面積;
![]() 在
在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得
,使得![]() 的值最大?若存在,直接寫出點
的值最大?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
![]() 當點
當點![]() 在雙曲線上運動時,作以
在雙曲線上運動時,作以![]() 、
、![]() 為鄰邊的平行四邊形,求平行四邊形周長最小時點
為鄰邊的平行四邊形,求平行四邊形周長最小時點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個關于![]() 的代數式
的代數式![]() ,若存在一個系數為正數關于
,若存在一個系數為正數關于![]() 的單項式
的單項式![]() ,使
,使![]() 的結果是所有系數均為整數的整式,則稱單項式
的結果是所有系數均為整數的整式,則稱單項式![]() 為代數式
為代數式![]() 的“整系單項式” ,例如:
的“整系單項式” ,例如:
當![]() 時,由于
時,由于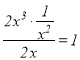 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于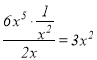 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于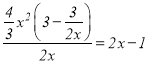 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于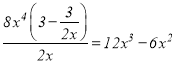 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
顯然,當代數式![]() 存在整系單項式
存在整系單項式![]() 時,
時,![]() 有無數個,現把次數最低,系數最小的整系單項式
有無數個,現把次數最低,系數最小的整系單項式![]() 記為
記為![]() ,例如:
,例如:![]() .
.
閱讀以上材料并解決下列問題:
⑴.判斷:當![]() 時,
時,![]()
![]() 的整系單項式(填“是”或“不是”);
的整系單項式(填“是”或“不是”);
⑵.當![]() 時,
時,![]() = ;
= ;
⑶.解方程: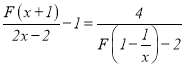 .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
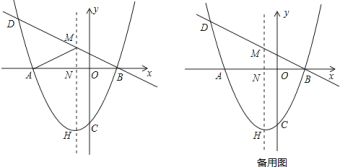
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,頂點為
,頂點為![]() ,其對稱軸交
,其對稱軸交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過
經過![]() 、
、![]() 兩點,交拋物線的對稱軸于點
兩點,交拋物線的對稱軸于點![]() ,其中點
,其中點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求拋物線的表達式;
(2)連接![]() ,求
,求![]() 的周長;
的周長;
(3)若![]() 是拋物線位于直線
是拋物線位于直線![]() 的下方且在其對稱軸左側上的一點,當四邊形
的下方且在其對稱軸左側上的一點,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
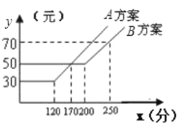
【題目】如圖,某電信公司提供了![]() ,
,![]() 兩種方案的移動通訊費用
兩種方案的移動通訊費用![]() (元)與通話時間
(元)與通話時間![]() (分)之間的關系,則以下說法正確的是( )
(分)之間的關系,則以下說法正確的是( )
①若通話時間少于120分,則![]() 方案比
方案比![]() 方案便宜
方案便宜
②若通話時間超過200分,則![]() 方案比
方案比![]() 方案便宜
方案便宜
③通訊費用為60元,則![]() 方案比
方案比![]() 方案的通話時間多
方案的通話時間多
④當通話時間是170分鐘/時,兩種方案通訊費用相等
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育器材室有A、B兩種型號的實心球,1只A型球與1只B型球的質量共7千克,3只A型球與1只B型球的質量共13千克.
(1)每只A型球、B型球的質量分別是多少千克?
(2)現有A型球、B型球的質量共17千克,則A型球、B型球各有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y1=(x-2)2+m與x軸交于點A和B,與y軸交于點C,點D是點C關于拋物線對稱軸的對稱點,若點A的坐標為(1,0),直線y2=kx+b經過點A,D.
(1)求拋物線的函數解析式;
(2)求點D的坐標和直線AD的函數解析式;
(3)根據圖象指出,當x取何值時,y2>y1.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了創建書香校園,去年又購進了一批圖書.經了解,科普書的單價比文學書的單價多4元,用1200元購進的科普書與用800元購進的文學書本數相等.
(1)求去年購進的文學羽和科普書的單價各是多少元?
(2)若今年文學書和科普書的單價和去年相比保持不變,該校打算用1000元再購進一批文學書和科普書,問購進文學書55本后至多還能購進多少本科普書?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC,DC⊥BC,E是BC上一點,使得AE⊥DE;
(1)求證:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的長;
(3)當△AED∽△ECD時,請寫出線段AD、AB、CD之間數量關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com