
【題目】
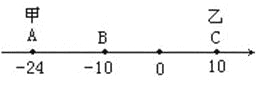
(1)甲、乙多少秒后相遇?
(2)甲出發多少秒后,甲到A、B、C三點的距離和為40個單位?
(3)當甲到A、B、C三點的距離和為40個單位時,甲調頭返回,當甲、乙在數軸上再次相遇時,相遇點表示的數是____________.
【答案】(1)3.4秒 (2)2或者5秒(3)-44
【解析】試題分析:(1)可設x秒后甲與乙相遇,根據甲與乙的路程差為34,可列出方程求解即可;
(2)設y秒后甲到A,B,C三點的距離之和為40個單位,分甲應為于AB或BC之間兩種情況討論即可求解;
(3)分①原點O是甲螞蟻P與乙螞蟻Q兩點的中點;②乙螞蟻Q是甲螞蟻P與原點O兩點的中點;③甲螞蟻P是乙螞蟻Q與原點O兩點的中點,三種情況討論即可求解.
試題解析:(1)設x秒后甲與乙相遇,則
4x+6x=34,
解得x=3.4,
甲乙在3.4秒后相遇.
(2)設y秒后甲到A,B,C三點的距離之和為40個單位,
B點距A,C兩點的距離為14+20=34<40,A點距B、C兩點的距離為14+34=48>40,C點距A、B的距離為34+20=54>40,故甲應為于AB或BC之間.
AB之間時:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之間時:4y+(4y-14)+(34-4y)=40,
解得y=5.
(3)①甲從A向右運動2秒時返回,設y秒后與乙相遇.此時甲、乙表示在數軸上為同一點,所表示的數相同.
甲表示的數為:-24+4×2-4y;乙表示的數為:10-6×2-6y,
依據題意得:-24+4×2-4y=10-6×2-6y,
解得:y=7,
相遇點表示的數為:-24+4×2-4y=-44(或:10-6×2-6y=-44),
②甲從A向右運動5秒時返回,設y秒后與乙相遇.
甲表示的數為:-24+4×5-4y;乙表示的數為:10-6×5-6y,
依據題意得:-24+4×5-4y=10-6×5-6y,
解得:y=-8(不合題意舍去),
即甲從A向右運動2秒時返回,能在數軸上與乙相遇,相遇點表示的數為-44.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某商店進行促銷活動,如果將進價為8元/件的商品按每件10元出售,每天可銷售100件,現采用提高售價,減少進貨量的辦法增加利潤,已知這種商品的單價每漲1元,其銷售量就要減少10件,問將售價定為多少元/件時,才能使每天所賺的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:b是最小的正整數,且a、b滿足![]() =0,請回答問題
=0,請回答問題
(1)請直接寫出a、b、c的值。
a=__________; b=__________;c=__________
(2)a、b、c所對應的點分別為A、B、C,點P為一動點,其對應的數為x,點P在0到2之間運動時(即0≤x≤2時),請化簡式子:![]() (請寫出化簡過程)
(請寫出化簡過程)
![]()
(3)在(1)(2)的條件下,點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和5個單位長度的速度向右運動,假設t秒鐘過后,若點B與點C之間的距離表示為BC,點A與點B之間的距離表示為AB。請問:BC-AB的值是否隨著時間t的變化而改變?若變化,請說明理由;若不變,請求其值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一次函數y=kx+b的圖象.
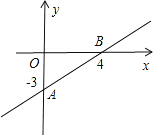
(1)求這個一次函數的解析式?
(2)試判斷點P(1,-1)是否在這個一次函數的圖象上?
(3)求原點O到直線AB的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高度發展,據調查,長沙市某家小型“大學生自主創業”的快遞公司,今年三月份與五月份完成投遞的快遞總件數分別為10萬件和12.1萬件,現假定該公司每月投遞的快遞總件數的增長率相同.
(1)求該快遞公司投遞總件數的月平均增長率;
(2)如果平均每人每月最多可投遞0.6萬件,那么該公司現有的21名快遞投遞業務員能否完成今年6月份的快遞投遞任務?如果不能,請問至少需要增加幾名業務員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若干個偶數按每行8個數排成如圖所示的陣列:

(1)圖中方框內的9個數的和與中間的數有什么關系?
(2)小亮畫了一個方框,他所畫的方框內9個數的和為360,求這9個數;(直接寫出答案)。
(3)小霞也畫了一個方框,方框內9個數的和為262,你能寫出這9個數嗎?如果不能,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大潤發超市進了一批成本為8元/個的文具盒。調查發現: 這種文具盒每個星期的銷售量![]() 個)與它的定價
個)與它的定價![]() (元/個)的關系如圖所示:
(元/個)的關系如圖所示:
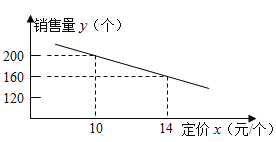
(1)求這種文具盒每個星期的銷售量![]() 個)與它的定價
個)與它的定價![]() (元/個)之間的函數關系式(不必寫出自變量
(元/個)之間的函數關系式(不必寫出自變量![]() 的取值范圍)
的取值范圍)
(2)每個文具盒定價是多少元時,超市每星期銷售這種文具盒(不考慮其他因素)可獲得的利潤最高?最高利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年3月5日,實驗中學組織全體學生參加了“走出校門,服務社會”的活動。九年級一班小明同學統計了該天本班學生打掃街道,去敬老院服務和到社區文藝演出的人數,并做了如下直方圖和扇形統計圖。請根據小明同學所作的兩個圖形,解答:
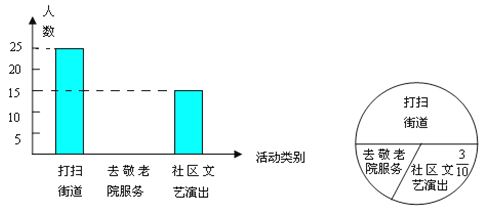
(1)九年級一班有多少名學生?
(2)補全直方圖的空缺部分。
(3)若九年級有800名學生,估計該年級去敬老院的人數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com