Question

【題目】如圖，排球運動員站在點O處練習發球，將球從O點正上方2 的A處發出，把球看成點，其運行的高度 與運行的水平距離 滿足關系式 ．已知球網與O點的水平距離為9 ，高度為2.43 ，球場的邊界距O點的水平距離為18 ．

（1）當 =2.6時，求 與 的關系式（不要求寫出自變量 的取值范圍）；
（2）當 =2.6時，球能否越過球網？球會不會出界？請說明理由；
（3）若球一定能越過球網，又不出邊界，求二次函數中 的取值范圍．

Answer 1

【答案】
（1）解：把 及 代入到 ， 當 時， y與x的關系式為
（2）解：當 時， ，因為當 , ,所以球能越過球網；當 時， 解得： （舍），故會出界
（3）解：當球正好過點（18,0）時，拋物線 還過點（0,2），代入解析式得： ，解得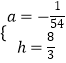： ，此時二次函數解析式為： 上次是球若不出邊界 當球剛能過網，此時函數解析式過 ，拋物線 還過點（0,2），代入解析式得：，解得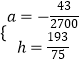： ，此時球要過網 故若要球一定能越過球網，又不出邊界， 的取值范圍為：
【解析】（1）把 x = 0 , y = 2 及 h = 2.6 代入關系式y = a + h中得到關于a的方程，解這個方程即可；（2）把h = 2.6代入解析式求出y的值與2．43 m比較大小即可判斷球能否越過球網，把y = 0代入解析式解得x的值與18比較大小即可判斷球會不會出界；（3）球若不出邊界 h ≥ ,球剛能過網，此時函數解析式過 ( 9 , 2.43 )代入解析式可得符合題意的值為： h ≥ 。