【題目】物華小區停車場去年收費標準如下：中型汽車的停車費為600元/輛，小型汽車的停車費為400元/輛，停滿車輛時能收停車費23000元，今年收費標準上調為：中型汽車的停車費為1000元/輛，小型汽車的停車費為600元/輛，若該小區停車場容納的車輛數沒有變化，今年比去年多收取停車費13000元.
（1）該停車場去年能停中、小型汽車各多少輛？
（2）今年該小區因建筑需要縮小了停車場的面積，停車總數減少了11輛，設該停車場今年能停中型汽車
輛，小型汽車有
輛，停車場收取的總停車費為
元，請求出關于的函數表達式；
（3）在（2）的條件下，若今年該停車場停滿車輛時小型汽車的數量不超過中型汽車的2倍，則今年該停車場最少能收取的停車費共多少元？
【答案】（1）該停車場去年能停中型汽車15輛，小型汽車35輛；（2）
；（3）今年該停車場最少能收取停車費共28600元．
【解析】
（1）設該停車場去年能停中型汽車
輛，小型汽車
輛，根據等量關系，列出二元一次方程組，即可求解；
（2）由題意得：
，根據“總停車費=中型汽車停車費+小型汽車費”，即可得到
關于的函數表達式；
（3）根據題意，列出關于x的不等式，得到x的取值范圍，再根據關于的函數表達式，即可求解．
（1）設該停車場去年能停中型汽車輛，小型汽車輛
根據題意，得：
，解得：
，
答：該停車場去年能停中型汽車15輛，小型汽車35輛；
（2）設該停車場去年能停中型汽車輛，小型汽車輛，
則
，
根據題意，得：
，
（3）由題意，得：
，，
∴
，解得：
．
∵
，
∴的值隨的增大而增大，
∴當
時，值最小，最小值為：
（元）．
答：今年該停車場最少能收取停車費共28600元．
科目：初中數學 來源： 題型：
【題目】下列命題的逆命題為假命題的是( )
A.如果一元二次方程
沒有實數根，那么
．
B.線段垂直平分線上任意一點到這條線段兩個端點的距離相等．
C.如果兩個數相等，那么它們的平方相等．
D.直角三角形兩條直角邊的平方和等于斜邊的平方．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為改善南寧市的交通現狀，市政府決定修建地鐵，甲、乙兩工程隊承包地鐵1號線的某段修建工作，從投標書中得知：甲隊單獨完成這項工程所需天數是乙隊單獨完成這項工程所需天數的3倍；若由甲隊先做20天，剩下的工程再由甲、乙兩隊合作10天完成．
求甲、乙兩隊單獨完成這項工程各需多少天？
已知甲隊每天的施工費用為
萬元，乙隊每天的施工費用為
萬元，工程預算的施工費用為500萬元，為縮短工期，擬安排甲、乙兩隊同時開工合作完成這項工程，那么工程預算的施工費用是否夠用？若不夠用，需增加多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題情境：課堂上，同學們研究幾何變量之間的函數關系問題：如圖，菱形ABCD的對角線AC，BD相交于點O，AC=4，BD=2．點P是AC上的一個動點，過點P作MN⊥AC，垂足為點P（點M在邊AD、DC上，點N在邊AB、BC上）．設AP的長為x（0≤x≤4），△AMN的面積為y．
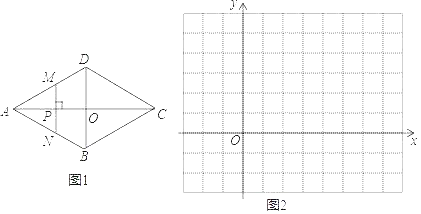
建立模型：（1）y與x的函數關系式為：
，
解決問題：（2）為進一步研究y隨x變化的規律，小明想畫出此函數的圖象．請你補充列表，并在如圖的坐標系中畫出此函數的圖象：
x | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y | 0 |
|
|
|
|
|
|
| 0 |
（3）觀察所畫的圖象，寫出該函數的兩條性質： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，一個長為
，寬為
的長方形，沿途中的虛線用剪刀均勻的分成四個小長方形，然后按圖②的形狀拼成一個正方形．
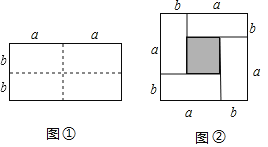
（1）觀察圖②，請用兩種不同的方法求圖②中陰影部分的面積．
方法1：________________________________________（只列式，不化簡）
方法2：________________________________________（只列式，不化簡）
（2）請寫出
三個式子之間的等量關系：_______________________________．
（3）根據（2）題中的等量關系，解決如下問題：若
，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
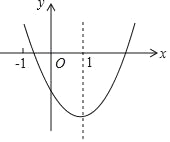
【題目】二次函數 y=ax2+bx+c（a≠0）的圖象如圖所示，對稱軸是直線 x=1，下列結論：①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0.其中正確的是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖
，圓柱的底面半徑為
，圓柱高
為
，
是底面直徑，求一只螞蟻從點
出發沿圓柱表面爬行到點
的最短路線，小明設計了兩條路線：
路線1：高線
底面直徑，如圖所示，設長度為
．
路線2：側面展開圖中的線段
，如圖
所示，設長度為
．
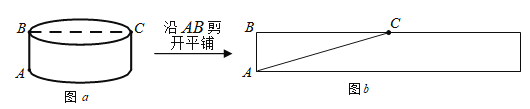
請按照小明的思路補充下面解題過程：
（1）解：
；
（2）小明對上述結論有些疑惑，于是他把條件改成：“圓柱底面半徑為，高為”繼續按前面的路線進行計算．（結果保留
）
①此時，路線1：__________．路線2：_____________．
②所以選擇哪條路線較短？試說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
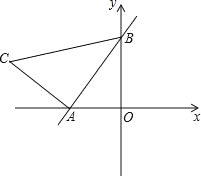
【題目】如圖，直線y=kx+2與x軸、y軸分別交于A、B兩點，OA：OB=
．以線段AB為邊在第二象限內作等腰Rt△ABC，∠BAC=90°．
（1）求點A的坐標和k的值；
（2）求點C坐標；
（3）直線y=x在第一象限內的圖象上是否存在點P，使得△ABP的面積與△ABC的面積相等？如果存在，求出點P坐標；如果不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
