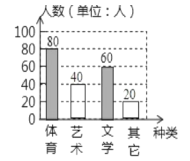
【題目】某校開設了豐富多彩的實踐類拓展課程,分別設置了體育類、藝術類、文學類及其它類課程(要求人人參與,每人只能選擇一門課程).為了解學生喜愛的拓展課類別,學校做了一次抽樣調查.根據收集到的數據,繪制成如下兩幅不完整的統計圖,請根據圖中提供的信息,完成下列問題：
(1)此次共調查了多少人?
(2)請將條形統計圖補充完整
(3)求文學類課程在扇形統計圖中所占圓心角的度數；
(4)若該校有1500名學生,請估計喜歡體育類拓展課的學生人數.
【答案】（1）200人；（2）畫圖見解析；（3）108°；（4）600人
【解析】
（1）結合兩個統計圖，根據體育類80人所占的百分比是40%，進行計算；
（2）根利用總人數乘以20%求得參加藝術社團的人數，再求得參加其它社團的人數，補全直方圖；
（3）利用360°乘以參加文學社團的所占的比例求得圓心角的度數；
（4）求出文學類所占的百分比，再用1500乘以百分比估計即可．
(1)調查的總人數是80÷40%=200(人)，
故答案是：200；
(2) 參加藝術社團的人數是200×20%=40(人)，
參加其它社團的人數200804060=20(人).
(3) 文學社團在扇形統計圖中所占圓心角的度數是360×
=108° .
(4)1500×40%=600(人).
∴估計該校喜歡體育類社團的學生有600人。
孟建平錯題本系列答案
超能學典應用題題卡系列答案科目：初中數學 來源： 題型：
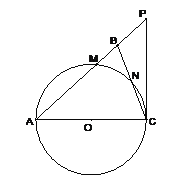
【題目】如圖，在△ABC中，∠ABC=∠ACB，以AC為直徑的⊙O分別交AB、BC于點M、N，點P在AB的延長線上，且∠CAB=2∠BCP.
（1）求證：直線CP是⊙O的切線；
（2）若BC=2
，sin∠BCP=
，求⊙O的半徑及△ACP的周長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，E、F分別是AD和BC上的兩點，EF將四邊形ABCD分成兩個邊長為5cm的正方形，∠DEF=∠EFB=∠B=∠D=90°;點H是CD上一點且CH=lcm，點P從點H出發，沿HD以lcm/s的速度運動，同時點Q從點A出發，沿A→B→C以5cm/s的速度運動.任意一點先到達終點即停止運動;連結EP、EQ.
(1)如圖1，點Q在AB上運動，連結QF，當t= 時，QF//EP;
(2)如圖2，若QE⊥EP，求出t的值;
(3)試探究:當t為何值時，
的面積等于
面積的
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的方程
（1）求證：不論k取什么實數值，這個方程總有實數根；
（2）若等腰三角形ABC的一邊長為
，另兩邊的長b、c恰好是這個方程的兩個根，求△ABC的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
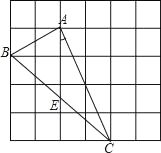
【題目】如圖，在邊長為1的小正方形組成的網格中，△ABC的三個頂點均在格點上，
請按要求完成下列各題：
（1）用2B鉛筆畫AD∥BC（D為格點），連接CD；
（2）線段CD的長為 ；
（3）請你在△ACD的三個內角中任選一個銳角，若你所選的銳角是 ，則它所對應的正弦函數值是 ；
（4）若E為BC中點，則tan∠CAE的值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，長方形ABCD是由六個正方形組成的完美長方形，中間最小正方形的面積是1，最大正方形的邊長為x.
(1)用x的代數式表示長方形ABCD的長是______或______、寬是______；
(2)求長方形ABCD的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
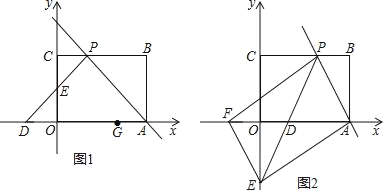
【題目】如圖1，矩形OABC擺放在平面直角坐標系中，點A在x軸上，點C在y軸上，OA＝3，OC＝2，過點A的直線交矩形OABC的邊BC于點P，且點P不與點B、C重合，過點P作∠CPD＝∠APB，PD交x軸于點D，交y軸于點E．
(1)若△APD為等腰直角三角形．
①求直線AP的函數解析式；
②在x軸上另有一點G的坐標為(2，0)，請在直線AP和y軸上分別找一點M、N，使△GMN的周長最小，并求出此時點N的坐標和△GMN周長的最小值．
(2)如圖2，過點E作EF∥AP交x軸于點F，若以A、P、E、F為頂點的四邊形是平行四邊形，求直線PE的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】直線 AB∥CD，直線 a 分別交 AB、CD 于點 E、F，點 M 在線段 EF 上，點 P 是 直線 CD 上的一個動點(點 P 不與點 F 重合)．
(1)如圖 1，當點 P 在射線 FC 上移動時，∠FMP＋∠FPM 與∠AEF 有什么數量關系？ 請說明理由；
(2)如圖 2，當點 P 在射線 FD 上移動時，∠FMP＋∠FPM 與∠AEF 有什么數量關系？ 請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知直角三角板
和直角三角板
,
,
,
.
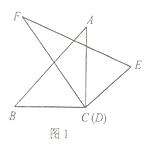
(1)如圖1,將頂點
和頂點
重合,保持三角板不動,將三角板繞點旋轉.當
平分
時,求
的度數；
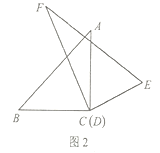
(2)在(1)的條件下,繼續旋轉三角板,猜想與
有怎樣的數量關系?并利用圖2所給的情形說明理由；
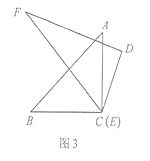
(3)如圖3,將頂點和頂點
重合,保持三角板不動,將三角板繞點旋轉.當
落在
內部時,直接寫出
與的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com