
【題目】如圖,一次函數y=kx+b(k≠0)與反比例函數y=![]() (m≠0)的圖象相交于A(2,3),B(-3,m)兩點.
(m≠0)的圖象相交于A(2,3),B(-3,m)兩點.
(1)求一次函數與反比例函數的解析式;
(2)根據所給條件,請直接寫出不等式kx+b>![]() 的解集;
的解集;
(3)過點B作BC⊥x軸,垂足為點C,求S△ABC.
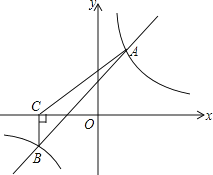
【答案】(1)反比例函數解析式為y=![]() ,一次函數解析式為y=x+1;(2)-3<x<0或x>2;(3)5.
,一次函數解析式為y=x+1;(2)-3<x<0或x>2;(3)5.
【解析】
(1)先把A點坐標代入y=![]() 可求出n的值,從而確定反比例函數解析式;再把B(-3,m)代入反比例函數解析式求出m的值,然后利用待定系數法求一次函數解析式;
可求出n的值,從而確定反比例函數解析式;再把B(-3,m)代入反比例函數解析式求出m的值,然后利用待定系數法求一次函數解析式;
(2)觀察函數圖象得到,當-3<x<0或x>2時,一次函數圖象在反比例函數圖象上方;
(3)先確定直線y=x+1與x軸交點D的坐標和C點坐標,然后利用S△ABC=S△DBC+S△ADC進行計算.
(1)把A(2,3)代入y=![]() 得n=2×3=6,
得n=2×3=6,
所以反比例函數解析式為y=![]() ,
,
把B(-3,m)代入y=![]() 得-3m=6,解得m=-2,則B點坐標為(-3,-2),
得-3m=6,解得m=-2,則B點坐標為(-3,-2),
把A(2,3)、B(-3,-2)代入y=kx+b得
![]() ,解得
,解得![]() ,
,
所以一次函數解析式為y=x+1;
(2)不等式kx+b>![]() 的解集為-3<x<0或x>2;
的解集為-3<x<0或x>2;
(3)如圖,直線y=x+1與x軸交點為D,則D(-1,0),
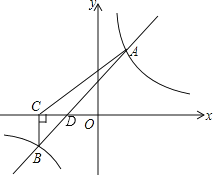
因為BC⊥x軸,
所以C點坐標為(-3,0),
所以S△ABC=S△DBC+S△ADC=![]() ×2×2+
×2×2+![]() ×2×3=5.
×2×3=5.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
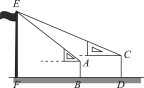
【題目】某校九年級某班開展數學活動,小明和小軍合作用一副三角板測量學校的旗桿,小明站在B點測得旗桿頂端E點的仰角為45°,小軍站在D點測得旗桿頂端E點的仰角為30°.已知小明和小軍的距離BD=6 m,小明的身高AB=1.5 m,小軍的身高CD=1.75 m,求旗桿的高EF.(結果精確到0.1,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽市精準扶貧工作已進入攻堅階段.貧困戶張大爺在某單位的幫扶下,把一片坡地改造后種植了優質水果藍莓,今年正式上市銷售.在銷售的30天中,第一天賣出20千克,為了擴大銷量,采取了降價措施,以后每天比前一天多賣出4千克.第x天的售價為y元/千克,y關于x的函數解析式為![]() 且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
(1)m= ,n= ;
(2)求銷售藍莓第幾天時,當天的利潤最大?最大利潤是多少?
(3)在銷售藍莓的30天中,當天利潤不低于870元的共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
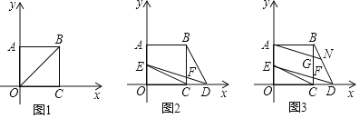
【題目】如圖,已知矩形OABC的一個頂點B的坐標是(4,2),反比例函數y=![]() (x>0)的圖象經過矩形的對稱中點E,且與邊BC交于點D,若過點D的直線y=mx+n將矩形OABC的面積分成3:5的兩部分,則此直線的解析式為_____.
(x>0)的圖象經過矩形的對稱中點E,且與邊BC交于點D,若過點D的直線y=mx+n將矩形OABC的面積分成3:5的兩部分,則此直線的解析式為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCO在平面直角坐標系中,AO,CO分別在y軸,x軸正半軸上,若S矩形AOCB=![]() BO2,矩形AOCB的周長為16.
BO2,矩形AOCB的周長為16.
(1)求B點坐標;
(2)點D在OC延長線上,設D點橫坐標為d,連BD,將直線DB繞D點逆時針方向旋轉45°交AO于E,交BC于F,連EC,設△CDE面積=S,求出S與d的函數關系式并注明自變量d的取值范圍;
(3)在(2)條件下,當點E在AO上時,過A作ED的平行線交CB于G,交BD于N,若BG=2CF,求S的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上一動點(不與點
邊上一動點(不與點![]() 重合),以
重合),以![]() 長為半徑的
長為半徑的![]() 與邊
與邊![]() 的另一個交點為
的另一個交點為![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .
.
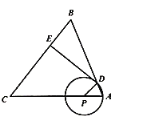
![]() 當
當![]() 與邊
與邊![]() 相切時,求
相切時,求![]() 的半徑;
的半徑;
![]() 聯結
聯結![]() 交
交![]() 于點
于點![]() ,設
,設![]() 的長為
的長為![]() ,
,![]() 的長為
的長為![]() ,求
,求![]() 關于
關于![]() 的函數解析式,并直接寫出
的函數解析式,并直接寫出![]() 的取值范圍;
的取值范圍;
![]() 在
在![]() 的條件下,當以
的條件下,當以![]() 長為直徑的
長為直徑的![]() 與
與![]() 相交于
相交于![]() 邊上的點
邊上的點![]() 時,求相交所得的公共弦的長.
時,求相交所得的公共弦的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在多項式的乘法公式中,完全平方公式![]() 是其中重要的一個.
是其中重要的一個.
(1)請補全完全平方公式的推導過程:
![]() ,
,
![]() ,
,
![]() .
.
(2)如圖,將邊長為![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,請你結合圖給出完全平方公式的幾何解釋.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,請你結合圖給出完全平方公式的幾何解釋.
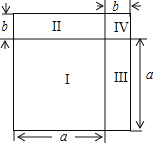
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點A為半圓O直徑MN所在直線上一點,射線AB垂直于MN,垂足為A,半圓繞M點順時針轉動,轉過的角度記作a;設半圓O的半徑為R,AM的長度為m,回答下列問題:
探究:(1)若R=2,m=1,如圖1,當旋轉30°時,圓心O′到射線AB的距離是 ;如圖2,當a= °時,半圓O與射線AB相切;
(2)如圖3,在(1)的條件下,為了使得半圓O轉動30°即能與射線AB相切,在保持線段AM長度不變的條件下,調整半徑R的大小,請你求出滿足要求的R,并說明理由.
(3)發現:(3)如圖4,在0°<α<90°時,為了對任意旋轉角都保證半圓O與射線AB能夠相切,小明探究了cosα與R、m兩個量的關系,請你幫助他直接寫出這個關系;
cosα= (用含有R、m的代數式表示)
拓展:(4)如圖5,若R=m,當半圓弧線與射線AB有兩個交點時,α的取值范圍是 ,并求出在這個變化過程中陰影部分(弓形)面積的最大值(用m表示)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com