
【題目】拋物線y=ax2+bx+c(a>0)經過點A(-3![]() ,0)、B(
,0)、B(![]() ,0),它與y軸相交于點C,且∠ACB≥90°,設該拋物線的頂點為D,△BCD的邊CD上的高為h.
,0),它與y軸相交于點C,且∠ACB≥90°,設該拋物線的頂點為D,△BCD的邊CD上的高為h.
(1)求實數a的取值范圍;
(2)求高h的取值范圍;
(3)當(1)的實數a取得最大值時,求此時△BCD外接圓的半徑.
【答案】(1)0<a≤![]() ;(2)0<h≤
;(2)0<h≤![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)利用直角三角形各邊的關系,求得OC2=OAOB,利用邊角關系,代入a值解得.
(2)過D作DE⊥OC,延長DC交x軸于點H,過點B作BF⊥CH于點F.利用頂點公式求得點D,由OC≤3,則tan∠OHC=![]() ≤
≤![]() ,從而解得.
,從而解得.
(3)求得a的最大值,求得h值,可得BD,BC,連接DG,由△DGB∽△BCF求得DG.
解:(1)當∠ACB=90°時,OC2=OAOB,
得OC=3
又∠ACB≥90°,
故OC≤3,
所以9a≤3,
∴0<a≤![]() .
.
(2)過D作DE⊥OC,延長DC交x軸于點H,過點B作BF⊥CH于點F.
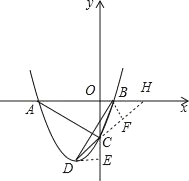
因為D為拋物線的頂點,
所以D(-![]() ,﹣12a),OE=12a,
,﹣12a),OE=12a,
又∵OC=9a,CE=3a,DE=![]() ,
,
易證△HCO∽△DCE,
有![]() =3,
=3,
故OH=3DE=3![]() ,BH=OH﹣OB=2
,BH=OH﹣OB=2![]() ,
,
又OC≤3,則tan∠OHC=![]() ≤
≤![]() ,
,
于是0<∠OHC<30°,
則h=BF=BHsin∠BHF≤BHsin30°=![]() ,
,
從而0<h≤![]() .
.
(3)當a取最大值時,a=![]() ,
,
此時h=![]() ,B(
,B(![]() ,0),C(0,﹣3),D(-
,0),C(0,﹣3),D(-![]() ,﹣4),
,﹣4),
可求BD=2![]() ,BC=2
,BC=2![]() ,
,
作直徑DG,易證△DGB∽△BCF,![]() ,
,

所以![]() .
.
故DG=4![]() ,
,
即△BCD外接圓的半徑為2![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx﹣3a經過點A(﹣1,0)、C(0,3),與x軸交于另一點B,拋物線的頂點為D.
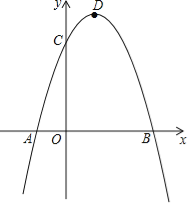
(1)求此二次函數解析式;
(2)連接DC、BC、DB,求證:△BCD是直角三角形;
(3)在對稱軸右側的拋物線上是否存在點P,使得△PDC為等腰三角形?若存在,求出符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
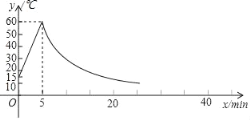
【題目】制作一種產品,需先將材料加熱達到60℃后,再進行操作,設該材料溫度為y(℃)從加熱開始計算的時間為x(min).據了解,當該材料加熱時,溫度y與時間x成一次函數關系:停止加熱進行操作時,溫度y與時間x成反比例關系(如圖).已知在操作加熱前的溫度為15℃,加熱5分鐘后溫度達到60℃.
(1)分別求出將材料加熱和停止加熱進行操作時,y與x的函數關系式;
(2)根據工藝要求,當材料的溫度低于15℃時,須停止操作,那么從開始加熱到停止操作,共經歷了多少時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華傳統文化,某校舉辦了學生“國學經典大賽”.比賽項目為:A.唐詩;B.宋詞;C.論語;D.三字經.比賽形式為“單人組”和“雙人組”.小紅和小明組成一個小組參加“雙人組”比賽,比賽規則是:同一小組的兩名隊員的比賽項目不能相同,且每人只能隨機抽取一次,則恰好小紅抽中“唐詩”且小明抽中“宋詞”的概率是多少?請用畫樹狀圖或列表的方法進行說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個梯子AB斜靠在一豎直的墻AO上,測得AO=2 m.若梯子的頂端沿墻下滑0.5米,這時梯子的底端也恰好外移0.5米,則梯子的長度AB為( )
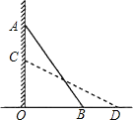
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區域為響應“綠水青山就是金山銀山”的號召,加強了綠化建設.為了解該區域群眾對綠化建設的滿意程度,某中學數學興趣小組在該區域的甲、乙兩個片區進行了調查,得到如下不完整統計圖.
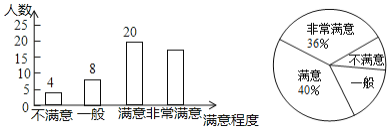
請結合圖中信息,解決下列問題:
(1)此次調查中接受調查的人數為多少人,其中“非常滿意”的人數為多少人;
(2)興趣小組準備從“不滿意”的4位群眾中隨機選擇2位進行回訪,已知這4位群眾中有2位來自甲片區,另2位來自乙片區,請用畫樹狀圖或列表的方法求出選擇的群眾來自甲片區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (x>0)交于點A,將直線y=
(x>0)交于點A,將直線y=![]() x向右平移3個單位后,與雙曲線y=
x向右平移3個單位后,與雙曲線y=![]() (x>0)交于點B,與x軸交于點C,若
(x>0)交于點B,與x軸交于點C,若![]() =2,則k=( )
=2,則k=( )

A. ![]() B. 4 C. 6 D.
B. 4 C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列關于函數![]() 的四個命題:
的四個命題:
①當x=0時,y有最小值6;
② m為任意實數,x=2-m時的函數值大于x=2+m時的函數值;
③若函數圖象過點(a,m0) 和(b, m0+1),其中a>0,b>2,則a<b;
④若m>2,且m是整數,當m≤x≤m+1 時,y的整數值有(2m-2)個.
其中真命題有______個.
查看答案和解析>>
科目:初中數學 來源: 題型:
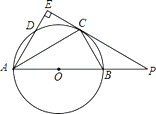
【題目】如圖,AB是⊙O的直徑,點C為⊙O上一點,AE和過點C的切線互相垂直,垂足為E,AE交⊙O于點D,直線EC交AB的延長線于點P,連接AC、BC.
(1)求證:AC平分∠BAD.
(2)求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com