
如圖所示,在△ABC中,AB=BC=2,∠ABC=120°,將△ABC繞點B順時針旋轉角a(0°<a<90°)得△A1BC1,A1B交AC于點E,A1C1分別交AC、BC于D、F兩點。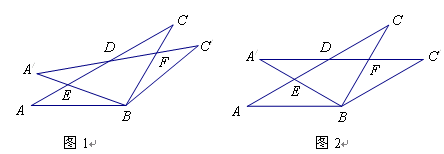
(1)如圖1,觀察并猜想,在旋轉過程中,線段EA1與FC有怎樣的數量關系?并證明你的結論;
(2)如圖2,當a=30°時,試判斷四邊形BC1DA的形狀,并說明理由;
(3)在(2)的情況下,求ED的長。
(1)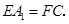 (2)四邊形
(2)四邊形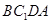 是菱形.(3)ED
是菱形.(3)ED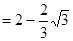
解析試題分析:(1)根據等邊對等角及旋轉的特征可得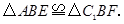 即可證得結論;
即可證得結論;
(2)先根據兩組對邊分別平行的四邊形是平行四邊形,再得到鄰邊相等即可判斷結論;
(3)過點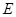 作
作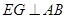 于點
于點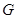 ,解
,解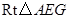 可得AE的長,結合菱形的性質即可求得結果。
可得AE的長,結合菱形的性質即可求得結果。
(1)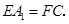
證明:(證法一)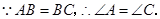
由旋轉可知,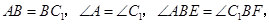
∴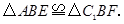
∴ 又
又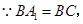
∴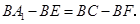 即
即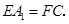
(證法二)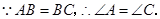
由旋轉可知,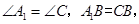 而
而
∴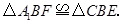
∴ ∴
∴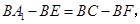
即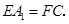
(2)四邊形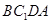 是菱形.
是菱形.
證明: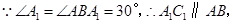 同理
同理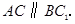
∴四邊形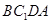 是平行四邊形.
是平行四邊形.
又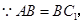 ∴四邊形
∴四邊形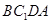 是菱形.
是菱形.
(3)過點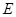 作
作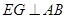 于點
于點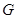 ,則
,則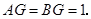

在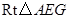 中,
中,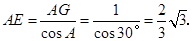
由(2)知四邊形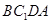 是菱形,
是菱形,
∴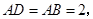
∴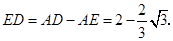
考點:本題考查的是旋轉的性質,菱形的判定與性質,解直角三角形
點評:解答本題的關鍵是掌握好旋轉的性質,平行四邊形判定與性質,的菱形的判定與性質,選擇適當的條件解決問題。


科目:初中數學 來源: 題型:
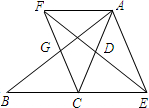 如圖所示,在△ABC中,D是AC的中點,E是線段BC延長線上一點,過點A作AF∥BC交ED的延長線于點F,連接AE,CF.
如圖所示,在△ABC中,D是AC的中點,E是線段BC延長線上一點,過點A作AF∥BC交ED的延長線于點F,連接AE,CF.查看答案和解析>>
科目:初中數學 來源: 題型:
 15、如圖所示,在△ABC中,DM、EN分別垂直平分AB和AC,交BC于D、E,若∠DAE=50°,則∠BAC=
15、如圖所示,在△ABC中,DM、EN分別垂直平分AB和AC,交BC于D、E,若∠DAE=50°,則∠BAC=查看答案和解析>>
科目:初中數學 來源: 題型:
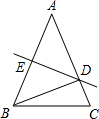 如圖所示,在△ABC中,AB=AC,DE是邊AB的垂直平分線,交AB于E,交AC于D,若△BCD的周長為18cm,△ABC的周長為30cm,那么BE的長為
如圖所示,在△ABC中,AB=AC,DE是邊AB的垂直平分線,交AB于E,交AC于D,若△BCD的周長為18cm,△ABC的周長為30cm,那么BE的長為查看答案和解析>>
科目:初中數學 來源: 題型:
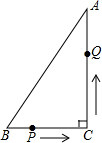 如圖所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P點在BC上從B點向C點運動(不包括點C),點P的運動速度為2cm∕s;Q點在AC上從C點向點A運動(不包括點A),運動速度為5cm∕s,若點P、Q分別從B、C同時運動,請解答下面的問題,并寫出主要過程.
如圖所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P點在BC上從B點向C點運動(不包括點C),點P的運動速度為2cm∕s;Q點在AC上從C點向點A運動(不包括點A),運動速度為5cm∕s,若點P、Q分別從B、C同時運動,請解答下面的問題,并寫出主要過程.| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com