
【題目】如圖,在平面直角坐標(biāo)系中,⊙D與y軸相切于點(diǎn)C(0,4),與x軸相交于A、B兩點(diǎn),且AB=6. 
(1)求圓的半徑和點(diǎn)D的坐標(biāo);
(2)點(diǎn)A的坐標(biāo)是 , 點(diǎn)B的坐標(biāo)是 , sin∠ACB;
(3)求經(jīng)過(guò)C、A、B三點(diǎn)的拋物線解析式;
(4)設(shè)拋物線的頂點(diǎn)為F,證明直線FA與⊙D相切.
【答案】
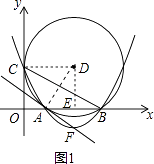
(1)解:過(guò)點(diǎn)D作DE⊥AB于E,連接DC、AD,如圖1,
則AE=EB= ![]() AB=3,DC⊥y軸,
AB=3,DC⊥y軸,
∴∠DCO=∠COE=∠DEO=90°,
∴四邊形OCDE是矩形,
∴OE=CD,DE=OC=4.
在Rt△ADE中,AD= ![]() =
= ![]() =5,
=5,
∴OE=CD=AD=5,
∴圓的半徑為5,點(diǎn)D的坐標(biāo)為(5,4);
(2)(2,0);(8,0);![]()
(3)解:設(shè)拋物線的解析式為y=ax2+bx+c,
∵A(2,0),B(8,0),C(0,4)在拋物線y=ax2+bx+c上,
∴  ,
,
解得 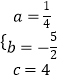 .
.
∴拋物線的解析式為y= ![]() x2﹣
x2﹣ ![]() x+4;
x+4;
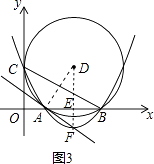
(4)解:連接DA,DF,如圖3,
∵D、F都在線段AB的垂直平分線上,
∴DF垂直平分AB.
由y= ![]() x2﹣
x2﹣ ![]() x+4=
x+4= ![]() (x﹣5)2﹣
(x﹣5)2﹣ ![]() 可得F(5,﹣
可得F(5,﹣ ![]() ),
),
∵DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() ,
,
∴DA2+AF2=52+( ![]() )2=
)2= ![]() =(
=( ![]() )2=DF2,
)2=DF2,
∴∠DAF=90°,
∴FA與⊙D相切.
【解析】解:(2)過(guò)點(diǎn)D作DE⊥AB于E,連接DB、AD,如圖2, 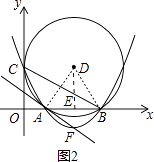
∵OE=5,AE=EB=3,
∴OA=5﹣3=2,OB=5+3=8.
∵DA=DB,
∴∠ADE=∠BDE= ![]() ∠ADB=∠ACB,
∠ADB=∠ACB,
∴sin∠ACB=sin∠ADE= ![]() =
= ![]() .
.
故答案分別為:(2,0),(8,0), ![]() ;
;
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解勾股定理的概念的相關(guān)知識(shí),掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在△ABC中,∠A=70°,∠B=90°,點(diǎn)A關(guān)于BC的對(duì)稱點(diǎn)是A',點(diǎn)B關(guān)于AC的對(duì)稱點(diǎn)是B',點(diǎn)C關(guān)于AB的對(duì)稱點(diǎn)是C',若△ABC的面積是![]() ,則△A'B'C'的面積是_________________________.
,則△A'B'C'的面積是_________________________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
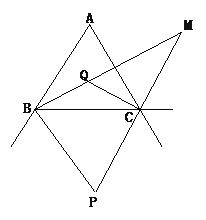
【題目】如圖,△ABC的兩外角平分線交于點(diǎn)P,易證∠P=90°-![]() ∠A;△ABC的兩內(nèi)角的平分線交于點(diǎn)Q,易證∠BQC=90°+
∠A;△ABC的兩內(nèi)角的平分線交于點(diǎn)Q,易證∠BQC=90°+![]() ∠A;那么△ABC的內(nèi)角平分線BM與外角平分CM的夾角∠M=_____∠A.
∠A;那么△ABC的內(nèi)角平分線BM與外角平分CM的夾角∠M=_____∠A.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在△ABC中,∠A=150°.第一步:在△ABC上方確定一點(diǎn)A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如圖1.第二步:在△A1BC上方確定一點(diǎn)A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如圖2.照此下去,至多能進(jìn)行( )步.
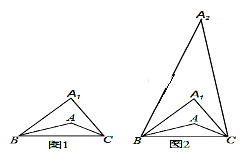
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在長(zhǎng)方形ABCD中,AB=4,AD=6.延長(zhǎng)BC到點(diǎn)E,使CE=3,連接DE,動(dòng)點(diǎn)P從點(diǎn)B出發(fā),以每秒1個(gè)單位的速度沿BC﹣CD﹣DA向終點(diǎn)A運(yùn)動(dòng),設(shè)點(diǎn)P的運(yùn)動(dòng)時(shí)間為t秒,當(dāng)t的值為__________秒時(shí).△ABP和△DCE全等.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)如圖①,在四邊形ABCD中,AB∥DC,E是BC的中點(diǎn),若AE是∠BAD的平分線,求證:AD=DC+AB,
(2)如圖②,在四邊形ABCD中,AB∥DC,F(xiàn)是DC延長(zhǎng)線上一點(diǎn),連接AF,E是BC的中點(diǎn),若AE是∠BAF的平分線,求證:AB=AF+CF.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD內(nèi)接于⊙O,點(diǎn)E在對(duì)角線AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度數(shù);
(2)求證:∠1=∠2.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)y= ![]() 的圖象如圖,以下結(jié)論:
的圖象如圖,以下結(jié)論:
①m<0;
②在每個(gè)分支上y隨x的增大而增大;
③若點(diǎn)A(﹣1,a)、點(diǎn)B(2,b)在圖象上,則a<b;
④若點(diǎn)P(x,y)在圖象上,則點(diǎn)P1(﹣x,﹣y)也在圖象上.
其中正確的個(gè)數(shù)是( )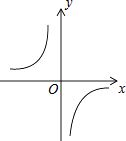
A.4個(gè)
B.3個(gè)
C.2個(gè)
D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)E在正方形ABCD的邊CD上,把△ADE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°至△ABF位置,如果AB= ![]() ,∠EAD=30°,那么點(diǎn)E與點(diǎn)F之間的距離等于 .
,∠EAD=30°,那么點(diǎn)E與點(diǎn)F之間的距離等于 . 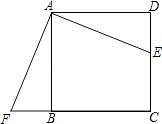
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com