
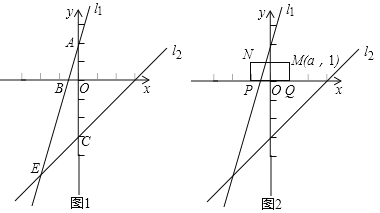
【題目】如圖1,在直角坐標系中,一次函數的圖象![]() 與
與![]() 軸交于點
軸交于點![]() ,與一次函數
,與一次函數![]() 的圖象
的圖象![]() 交于點
交于點![]() .
.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與y軸交于點
與y軸交于點![]() ,求四邊形
,求四邊形![]() 的面積;
的面積;
(3)如圖2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的邊
的邊![]() 在
在![]() 軸上平移,若矩形
軸上平移,若矩形![]() 與直線
與直線![]() 或
或![]() 有交點,直接寫出
有交點,直接寫出![]() 的取值范圍,
的取值范圍,
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由點![]() 在一次函數
在一次函數![]() 圖象上可求出E點坐標,然后將AE兩點坐標代入解析式即可求出l1的表達式;
圖象上可求出E點坐標,然后將AE兩點坐標代入解析式即可求出l1的表達式;
(2)由于![]() ,求出BC坐標即可解答
,求出BC坐標即可解答
(3)分別求出矩形MNPQ與直線l1或l2有交點邊界時的極限值可解答
(1)∵點![]() 在一次函數
在一次函數![]() 圖象上,
圖象上,
∴![]() ,
,
∴![]() ;
;
設直線![]() 的表達式為
的表達式為![]() ,
,
∵直線![]() 過點
過點![]() 和
和![]() ,
,
∴![]() ,
,
解得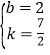 .
.
∴直線![]() 的表達式為
的表達式為![]() .
.
(2)由(1)可知:![]() 點坐標為
點坐標為![]() ,
,![]() 點坐標為
點坐標為![]() ,
,
∴![]()
![]() .
.
(3)![]() 或
或![]() .
.
當Q在直線![]() 上時,a=
上時,a=![]() ,此時矩形MNPQ與直線
,此時矩形MNPQ與直線![]() 有交點a取最小值,
有交點a取最小值,
當N在直線![]() 上時,N點坐標=
上時,N點坐標=![]() ,a=
,a=![]() ,此時矩形MNPQ與直線
,此時矩形MNPQ與直線![]() 有交點a取最大值,
有交點a取最大值,
當Q在直線![]() 上時,a=2,此時矩形MNPQ與直線
上時,a=2,此時矩形MNPQ與直線![]() 有交點a取最小值,
有交點a取最小值,
當N在直線![]() 上時,N點坐標=4,a=6,此時矩形MNPQ與直線
上時,N點坐標=4,a=6,此時矩形MNPQ與直線![]() 有交點a取最大值,
有交點a取最大值,
故當![]() 時,矩形MNPQ與直線
時,矩形MNPQ與直線![]() 有交點,當2≤a≤6時,矩形MNPQ與直線
有交點,當2≤a≤6時,矩形MNPQ與直線![]() 有交點,
有交點,


科目:初中數學 來源: 題型:
【題目】某大學公益組織計劃購買![]() 兩種的文具套裝進行捐贈,關注留守兒童經洽談,購買
兩種的文具套裝進行捐贈,關注留守兒童經洽談,購買![]() 套裝比購買
套裝比購買![]() 套裝多用20元,且購買5套
套裝多用20元,且購買5套![]() 套裝和4套
套裝和4套![]() 套裝共需820元.
套裝共需820元.
(1)求購買一套![]() 套裝文具、一套
套裝文具、一套![]() 套裝各需要多少元?
套裝各需要多少元?
(2)根據該公益組織的募捐情況和捐助對象情況,需購買![]() 兩種套裝共60套,要求購買
兩種套裝共60套,要求購買![]() 兩種套裝的總費用不超過5240元,則購買
兩種套裝的總費用不超過5240元,則購買![]() 套裝最多多少套?
套裝最多多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
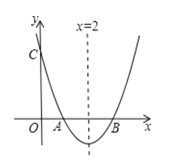
【題目】如圖,已知拋物線y=x2+bx+c與x軸交于點A,B,AB=2,與y軸交于點C,對稱軸為直線x=2.
(1)求拋物線的函數表達式;
(2)根據圖像,直接寫出不等式x2+bx+c>0的解集: .
(3)設D為拋物線上一點,E為對稱軸上一點,若以點A,B,D,E為頂點的四邊形是菱形,則點D的坐標為: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,有一個由六個邊長為1的正方形組成的圖案,其中點A,B的坐標分別為(3,5),(6,1).若過原點的直線l將這個圖案分成面積相等的兩部分,則直線l的函數解析式為_____.
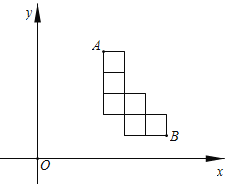
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 拋物線![]() 與
與![]() 軸交于點A(-1,0),頂點坐標(1,n)與
軸交于點A(-1,0),頂點坐標(1,n)與![]() 軸的交點在(0,2),(0,3)之間(包 含端點),則下列結論:①
軸的交點在(0,2),(0,3)之間(包 含端點),則下列結論:①![]() ;②
;②![]() ;③對于任意實數m,
;③對于任意實數m,![]() 總成立;④關于
總成立;④關于![]() 的方程
的方程![]() 有兩個不相等的實數根.其中結論正確的個數為
有兩個不相等的實數根.其中結論正確的個數為![]()
![]()

A. 1 個 B. 2 個 C. 3 個 D. 4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解七年級1000名學生的身體健康情況,從該年級隨機抽取了若干名學生,將他們按體重(均為整數,單位:kg)分成五組(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依據統計數據繪制了如下兩幅尚不完整的統計圖.

請解答下列問題:
(1)這次隨機抽取了 名學生調查,并補全頻數分布直方圖;
(2)在抽取調查的若干名學生中體重在 組的人數最多,在扇形統計圖中D組的圓心角是 度;
(3)請你估計該校七年級體重超過60kg的學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年購物的支付方式日益增多,某數學興趣小組就此進行了抽樣調查.調查結果顯示,支付方式有:A微信、B支付寶、C現金、D其他,該小組對某超市一天內購買者的支付方式進行調查統計,得到如下兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次一共調查了多少名購買者?
(2)請補全條形統計圖;在扇形統計圖中A種支付方式所對應的圓心角為 度.
(3)若該超市這一周內有1600名購買者,請你估計使用A和B兩種支付方式的購買者共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解決問題:
材料1:對于一個三位數其十位數字等于個位數字與百位數字的差的兩倍,則我們稱這樣的數為“倍差數”如122,![]() ;
;
材料2:若一個數![]() 能夠寫成
能夠寫成![]() 均為正整數,且
均為正整數,且![]() ,則我們稱這樣的數為“不完全平方差數”,
,則我們稱這樣的數為“不完全平方差數”,![]() 最大時,我們稱此時的
最大時,我們稱此時的![]() 、
、![]() 為
為![]() 的一組“最優分解數”,井規定
的一組“最優分解數”,井規定![]() .例如
.例如![]() ,因為:
,因為:![]() ,
,![]() ,
,![]() ,所以
,所以![]() ;
;
(1)求證:任意的一個“倍差數”與其百位數字之和能夠被3整除;
(2)若一個小于300的三位數![]() 其中
其中![]() ,
,![]() ,且
,且![]() 均為整數)既是一個“不完全平方差數”,也是一個“倍差數”,求所有
均為整數)既是一個“不完全平方差數”,也是一個“倍差數”,求所有![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com