
【題目】學校組織甲、乙兩組同學參加國學經典知識對抗賽,每組有![]() 位選手,每場比賽兩組各派
位選手,每場比賽兩組各派![]() 人進行現場對抗比賽,滿分為
人進行現場對抗比賽,滿分為![]() 分,共進行了
分,共進行了![]() 場比賽.學校整理和匯總了這
場比賽.學校整理和匯總了這![]() 場比賽的成績,并制成如下所示的尚不完整的統計表和圖所示的折線統計圖.
場比賽的成績,并制成如下所示的尚不完整的統計表和圖所示的折線統計圖.
場次 | 一 | 二 | 三 | 四 | 五 | 六 |
甲組成績 (單位:分) |
|
|
|
|
|
|
乙組成績 (單位:分) |
|
|
|
|
|
|
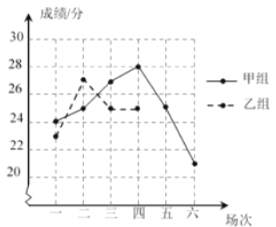
根據以上信息回答下面的問題:
(1)若甲、乙兩組成績的平均數相同,
①求![]() 的值;
的值;
②將折線統計圖補充完整,并根據折線統計圖判斷哪組成績比較穩定.
(2)若甲、乙兩組成績的中位數相等,直接寫出![]() 的最小值.
的最小值.
(3)在(1)中的條件下,若從所有成績為![]() 分的選手中隨機抽取兩人對其答題情況進行分析,請用列表法求抽到的兩位選手均來自同一組的概率.
分的選手中隨機抽取兩人對其答題情況進行分析,請用列表法求抽到的兩位選手均來自同一組的概率.
【答案】(1)①![]() ;②圖見解析,乙組成績較穩定;(2)
;②圖見解析,乙組成績較穩定;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)①首先根據“甲、乙兩組成績的平均數相同”可以得出甲、乙兩組的總分數一樣,據此列出方程求解即可;②根據已經計算出的![]() 的值再結合表格信息進一步補全圖形,由此再根據折線波動情況進行分析比較即可;
的值再結合表格信息進一步補全圖形,由此再根據折線波動情況進行分析比較即可;
(2)首先根據中位數的定義求出甲組的中位數,然后進一步根據乙組成績加以分析即可;
(3)根據題意,根據列表法找出所有可能發生的事件,然后進一步求出相應的概率即可.
(1)①∵甲、乙兩組成績的平均數相同,
∴![]() ,
,
解得,![]() ;
;
②補全折線統計圖如下圖所示:
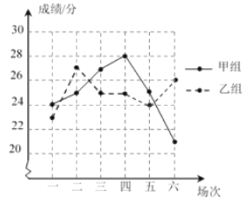
從折線統計圖中可以看出乙組的成績波動較小,
∴乙組的成績比較穩定;
(2)將甲組成績按從小到大排列可得:21,24,25,25,27,28,
∴甲組成績的中位數為:25,
即乙組的成績的中位數也是25,
然后將乙組的成績除去![]() 外按照從小到大順序排列可得:23,24,25,25,27,
外按照從小到大順序排列可得:23,24,25,25,27,
∵乙組的成績的中位數也是25,
∴![]() ,
,
∴![]() 的最小值為
的最小值為![]() ;
;
(3)根據題意,在(1)中的條件下,甲、乙兩組各有兩位選手的成績為![]() 分,設甲組的這兩位選手分別記作甲1、甲2,乙組的這兩位選手分別記作乙1、乙2,列表如下:
分,設甲組的這兩位選手分別記作甲1、甲2,乙組的這兩位選手分別記作乙1、乙2,列表如下:
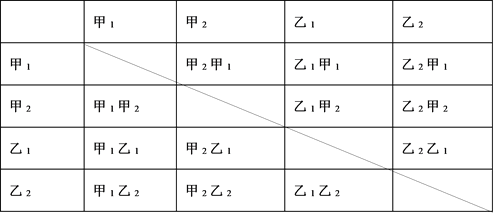
根據列表可知,一共有![]() 種等可能的情況,其中得分為
種等可能的情況,其中得分為![]() 分的兩位選手均來自同一組共有
分的兩位選手均來自同一組共有![]() 種情況,故
種情況,故![]() (兩位選手均來自同一組)
(兩位選手均來自同一組)![]() .
.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案科目:初中數學 來源: 題型:
【題目】某水果商販用600元購進了一批水果,上市后銷售非常好,商販又用1400元購進第二批這種水果,所購水果數量是第一批購進數量的2倍,但每箱進價多了5元.
(1)求該商販第一批購進水果每箱多少元;
(2)由于儲存不當,第二批購進的水果中有10%腐壞,不能售賣,該商販將兩批水果按同一價格全部銷售完畢后獲利不低于800元,求每箱水果的售價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
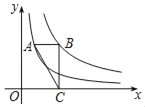
【題目】如圖,點A在反比例函數y=![]() (x>0)的圖象上,點B在反比例函數y=
(x>0)的圖象上,點B在反比例函數y=![]() (x>0)的圖象上,AB∥x軸,BC⊥x軸,垂足為C,連接AC,若△ABC的面積為2,則k的值為_____.
(x>0)的圖象上,AB∥x軸,BC⊥x軸,垂足為C,連接AC,若△ABC的面積為2,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
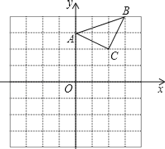
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)以點B為位似中心,在網格內畫出△A1B1C1,使△A1B1C1與△ABC位似,且位似比為2:1,點C1的坐標是_______;
(2)△A1B1C1的面積是_______平方單位.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“一帶一路”倡議提出五年多來,交通、通信、能源等各項相關建設取得積極進展,也為增進各國民眾福祉提供了新的發展機遇.下圖是2017年“一年一路”沿線部分國家的通信設施現狀統計圖.
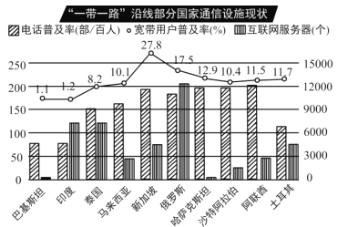
根據統計圖提供的信息,下列推斷合理的是( ).
A.互聯網服務器擁有個數最多的國家是阿聯酋
B.寬帶用戶普及率的中位數是11.05%
C.有8個國家的電話普及率能夠達到平均每人1部
D.只有俄羅斯的三項指標均超過了相應的中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是![]() 的直徑,點P在BA的延長線上,PD切
的直徑,點P在BA的延長線上,PD切![]() 于點D,過點B作
于點D,過點B作![]() ,交PD的延長線于點C,連接AD并延長,交BE于點E.
,交PD的延長線于點C,連接AD并延長,交BE于點E.
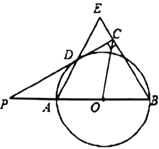
(Ⅰ)求證:AB=BE;
(Ⅱ)連結OC,如果PD=2![]() ,∠ABC=60°,求OC的長.
,∠ABC=60°,求OC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D是BC的中點,E是AD的中點,過點A作AF∥BC交BE的延長線于點F.

(1)求證:四邊形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com