
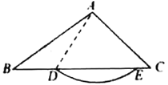
【題目】在![]() 中,D是邊BC上一點,以點A為圓心,AD長為半徑作弧,如果與邊BC有交點E(不與點D重合),那么稱
中,D是邊BC上一點,以點A為圓心,AD長為半徑作弧,如果與邊BC有交點E(不與點D重合),那么稱![]() 為
為![]() 的A-外截弧.例如,圖中
的A-外截弧.例如,圖中![]() 是
是![]() 的一條A-外截弧.在平面直角坐標系xOy中,已知
的一條A-外截弧.在平面直角坐標系xOy中,已知![]() 存在A-外截弧,其中點A的坐標為
存在A-外截弧,其中點A的坐標為![]() ,點B與坐標原點O重合.
,點B與坐標原點O重合.
(1)在點![]() ,
,![]() ,
,![]() ,
,![]() 中,滿足條件的點C是_______.
中,滿足條件的點C是_______.
(2)若點C在直線![]() 上.
上.
①求點C的縱坐標的取值范圍.
②直接寫出![]() 的A-外截弧所在圓的半徑r的取值范圍.
的A-外截弧所在圓的半徑r的取值范圍.
【答案】(1)C2、C3;(2)-2<y<![]() 或y>2;(3)
或y>2;(3)![]() <r<5或
<r<5或![]() <r<5.
<r<5.
【解析】
(1)如圖,根據BC1⊥AB可得△ABC1沒有A-外截弧,作AF⊥BC2于F,由AC2<AB可得當AF<AD2<AC2時,△ABC2有A-外截弧;作AG⊥BC3于G,根據點C3坐標,可求出AC3的長,可得AC3<AB,即可得出AG<AD1<AC3時,△ABC3有A-外截弧;根據A、B、C4坐標可求出BC4、AC4的長,根據勾股定理逆定理可得△ABC4是直角三角形,且AC4⊥BC4,可得△ABC4沒有A-外截弧,綜上即可得答案;
(2)①根據△ABC有A-外截弧可得∠ABC<90°,可得x>0,設點C坐標為(m,m-2),利用直角三角形斜邊中線的性質可求出∠ACB=90°時點C的坐標,根據∠ACB<90°時,△ABC有A-外截弧可得m的取值范圍,代入y=x-2,即可得點C縱坐標的取值范圍;
②求出∠ACB=90°時AC的長,進而可得答案.
(1)如圖,∵BC1⊥AB,
∴△ABC1沒有A-外截弧,
作AF⊥BC2于F,
∵A(5,0),B(0,0),C2(5,-3),
∴∠BAC2=90°,AC2=3,AB=5,
∴AC2<AB,
∴AF<AD2<AC2時,△ABC2有A-外截弧,滿足條件,
作AG⊥BC3于G,
∵C3(6,4),
∴AC3=![]() <AB,
<AB,
∴AG<AD1<![]() 時,△ABC3有A-外截弧,滿足條件,
時,△ABC3有A-外截弧,滿足條件,
∵C4(4,2),
∴BC4=![]() ,AC4=
,AC4=![]() ,AB=5,
,AB=5,
∵(![]() )2+(
)2+(![]() )2=52,
)2=52,
∴△ABC4是直角三角形,∠AC4B=90°,
∴△ABC4沒有A-外截弧,
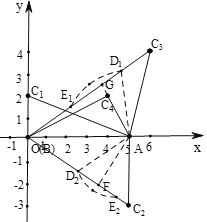
綜上所述:滿足條件的點C是C2、C3.
故答案為:C2、C3
(2)①∵點C在直線y=x-2上,
∴設點C的坐標為(m,m-2),
∵△ABC有A-外截弧,
∴∠ABC<90°,
∴m>0,
當∠ACB=90°時,
∵A(5,0),B(0,0),
∴斜邊AB的中點H的坐標為(2.5,0),
∴(m-2.5)2+(m-2)2=(2.5)2,
解得:m1=![]() ,m2=4,
,m2=4,
∴∠ACB=90°時,點C坐標為(![]() ,
,![]() )或(4,2),
)或(4,2),
∵直線解析式為y=x-2,
∴x=0時,y=-2,
∴與y軸交點為(0,-2),
∵△ABC有A-外截弧時,∠ACB<90°,
∴點C的縱坐標的取值范圍為-2<y<![]() 或y>2.
或y>2.
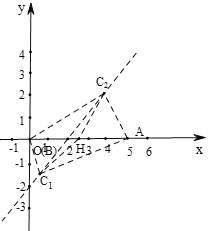
②由①得x=![]() 或x=4時,∠ACB=90°,
或x=4時,∠ACB=90°,
∴C1(![]() ,
,![]() ),C2(4,2),
),C2(4,2),
∴AC1=![]() ,AC2=
,AC2=![]() ,
,
∴![]() 的A-外截弧所在圓的半徑r的取值范圍為:
的A-外截弧所在圓的半徑r的取值范圍為:![]() <r<5或
<r<5或![]() <r<5.
<r<5.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
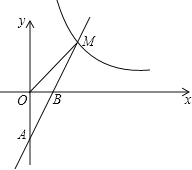
【題目】如圖,一次函數![]() 的圖象經過
的圖象經過![]() ,
,![]() 兩點,與反比例函數
兩點,與反比例函數![]() 的圖象在第一象限內的交點為
的圖象在第一象限內的交點為![]() .
.
![]() 求一次函數和反比例函數的表達式;
求一次函數和反比例函數的表達式;
![]() 在x軸上是否存在點P,使
在x軸上是否存在點P,使![]() ?若存在,求出點P的坐標;若不存在,說明理由.
?若存在,求出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
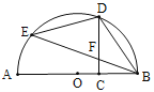
【題目】如圖,AB是⊙O的直徑,C是線段OB上的一點(不與點B重合),D,E是半圓上的點且CD與BE交于點F,用①![]() ,②DC⊥AB,③FB=FD中的兩個作為題設,余下的一個作為結論組成一個命題,則組成真命題的個數為( )
,②DC⊥AB,③FB=FD中的兩個作為題設,余下的一個作為結論組成一個命題,則組成真命題的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 上部分點的橫坐標x與縱坐標y的對應值如下表
上部分點的橫坐標x與縱坐標y的對應值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列結論:①拋物線開口向下;②當![]() 時,y隨x的增大而減小;③拋物線的對稱軸是直線
時,y隨x的增大而減小;③拋物線的對稱軸是直線![]() ;④函數
;④函數![]() 的最大值為2.其中所有正確的結論為( )
的最大值為2.其中所有正確的結論為( )
A.①②③B.①③C.①③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,B是![]() 的半徑OA上的一點(不與端點重合),過點B作OA的垂線交
的半徑OA上的一點(不與端點重合),過點B作OA的垂線交![]() 于點C,D,連接OD,E是
于點C,D,連接OD,E是![]() 上一點,
上一點,![]() ,過點C作
,過點C作![]() 的切線l,連接OE并延長交直線l于點F.
的切線l,連接OE并延長交直線l于點F.
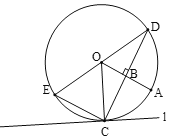
(1)①依題意補全圖形.
②求證:∠OFC=∠ODC.
(2)連接FB,若B是OA的中點,![]() 的半徑是4,求FB的長.
的半徑是4,求FB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
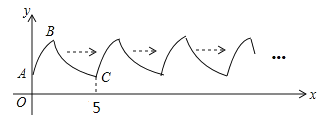
【題目】如圖,曲線AB是拋物線![]() 的一部分(其中A是拋物線與y軸的交點,B是頂點),曲線BC是雙曲線
的一部分(其中A是拋物線與y軸的交點,B是頂點),曲線BC是雙曲線![]() 的一部分.曲線AB與BC組成圖形W由點C開始不斷重復圖形W形成一組“波浪線”.若點
的一部分.曲線AB與BC組成圖形W由點C開始不斷重復圖形W形成一組“波浪線”.若點![]() ,
,![]() 在該“波浪線”上,則m的值為________,n的最大值為________.
在該“波浪線”上,則m的值為________,n的最大值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地質量監管部門對轄區內的甲、乙兩家企業生產的某同類產品進行檢查,分別隨機抽取了50件產品并對某一項關鍵質量指標做檢測,獲得了它們的質量指標值s,并對樣本數據(質量指標值s)進行了整理、描述和分析.下面給出了部分信息.
a.該質量指標值對應的產品等級如下:
質量指標值 |
|
|
|
|
|
等級 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
說明:等級是一等品,二等品為質量合格(其中等級是一等品為質量優秀).
等級是次品為質量不合格.
b.甲企業樣本數據的頻數分布統計表如下(不完整).
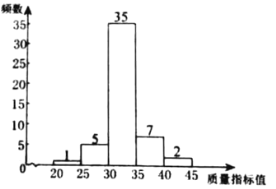
c.乙企業樣本數據的頻數分布直方圖如下.
甲企業樣本數據的頻數分布表
分組 | 頻數 | 頻率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合計 | 50 | 1.00 |
乙企業樣本數據的頻數分布直方圖
d.兩企業樣本數據的平均數、中位數、眾數、極差、方差如下:
平均數 | 中位數 | 眾數 | 極差 | 方差 | |
甲企業 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企業 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根據以上信息,回答下列問題:
(1)m的值為________,n的值為________.
(2)若從甲企業生產的產品中任取一件,估計該產品質量合格的概率為________;若乙企業生產的某批產品共5萬件,估計質量優秀的有________萬件;
(3)根據圖表數據,你認為________企業生產的產品質量較好,理由為______________.(從某個角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB為⊙O的直徑.
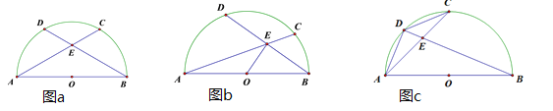
(1)如圖a,點D為![]() 的中點,當弦BD=AC時,求∠A.
的中點,當弦BD=AC時,求∠A.
(2)如圖b,點D為![]() 的中點,當AB=6,點E為BD的中點時,求OE的長.
的中點,當AB=6,點E為BD的中點時,求OE的長.
(3)如圖c,點D為![]() 上任意一點(不與A、C重合),若點C為
上任意一點(不與A、C重合),若點C為![]() 的中點,探求BD、AD、CD之間的數量關系,直接寫出你探求的結論,不要求證明.
的中點,探求BD、AD、CD之間的數量關系,直接寫出你探求的結論,不要求證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,半徑OC=6,D是半徑OC上一點,且 OD=4.A,B是⊙O上的兩個動點,∠ADB=90°,F是AB的中點,則OF的長的最大值等于______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com