【題目】如圖，AE是圓O的直徑，點B在AE的延長線上，點D在圓O上，且AC⊥DC， AD平分∠EAC
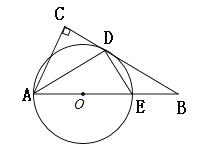
(1)求證：BC是圓O的切線。
(2)若BE=8,BD=12,求圓O的半徑,
【答案】（1）證明見解析；（2）10.
【解析】
試題（1）要證DE是⊙O的切線，只要連接OC，再證∠DCO=90°即可．
（2）已知兩邊長，求其它邊的長，可以來三角形相似，對應邊成比例來求．
試題解析：（1）證明：連接OC；
∵AD平分∠EAC，
∴∠CAD=∠BAD；
又在圓中OA=OD，
∴∠AD0=∠OAD，
∴∠CAD=∠ADO，
∴AC∥OD；
則由AE⊥DC知OC⊥DC，
即DC是⊙O的切線．
（2）解：∵∠B=∠B，∠DAE=∠BDE，
∴△BDE∽△BAE，
∴
，
∴BD2=BE·BA，
即：BD2=BE·（BE+EA），
∴122=8(8+AE)
∴AE=10.
考點: 1.切線的判定；2.相似三角形的判定與性質.
目標測試系列答案科目：初中數學 來源： 題型：
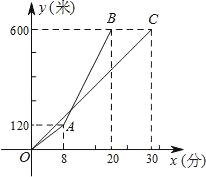
【題目】甲、乙兩人沿同一路線登山，圖中線段OC、折線OAB分別是甲、乙兩人登山的路程y（米）與登山時間x（分）之間的函數圖象．請根據圖象所提供的信息，解答如下問題：
（1）求甲登山的路程與登山時間之間的函數關系式，并寫出自變量x的取值范圍；
（2）求乙出發后多長時間追上甲？此時乙所走的路程是多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
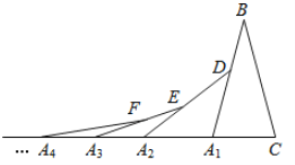
【題目】如圖，在第1個
中，
，
；在邊
上任取一點
，延長
到
，使
，得到第2個
；在邊
上任取一點
，延長
到
，使
．得到第3個
．．．按此做法繼續下去，則第
個三角形中以
為頂點的內角度數是( )
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
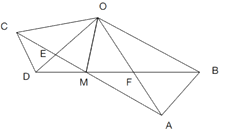
【題目】如圖，在
和
中，
連接AC，BD交于點M，AC與OD相交于E，BD與OA相較于F，連接OM，則下列結論中：①
；②
；③
；④MO平分
，正確的個數有( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB為⊙O的直徑，C為⊙O上一點，CD⊥AB于D，AD=9，BD=4，以C為圓心，CD為半徑的圓與⊙O相交于P，Q兩點，弦PQ交CD于E，則PEEQ的值是（ )
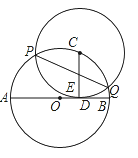
A. 24 B. 9 C. 36 D. 27
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】四邊形
是平行四邊形，點
在
邊上運動（點不與點
，
重合）
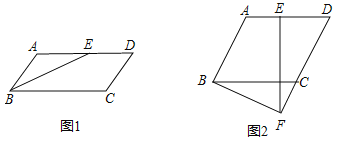
（1）如圖1，當點運動到邊的中點時，連接
，若平分
，證明：
；
（2）如圖2，過點作
且交
的延長線于點
，連接
．若
，
，
，在線段
上是否存在一點
，使得四邊形
是菱形？若存在，請說明當發，點分別在線段，上什么位置時四邊形是菱形，并證明；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，一幢樓房AB背后有一臺階CD，臺階每層高0.2米，且AC＝17.2米，設太陽光線與水平地面的夾角為α，當α＝60°時，測得樓房在地面上的影長AE＝10米，現有一老人坐在MN這層臺階上曬太陽．（
取1.73）
（1）求樓房的高度約為多少米？
（2）過了一會兒，當α＝45°時，問老人能否還曬到太陽？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是半圓O的直徑，過點O作弦AD的垂線交半圓O于點E，交AC于點C，使∠BED=∠C．
（1）判斷直線AC與圓O的位置關系，并證明你的結論；
（2）若AC=8，cos∠BED=
，求AD的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
