
【題目】閱讀與理解: 圖1是邊長分別為a和b(a>b)的兩個等邊三角形紙片ABC和C′DE疊放在一起(C與C′重合)的圖形.
操作與證明:
(1)操作:固定△ABC,將△C′DE繞點(diǎn)C按順時針方向旋轉(zhuǎn)30°,連接AD,BE,如圖2;在圖2中,線段BE與AD之間具有怎樣的大小關(guān)系?證明你的結(jié)論; 
(2)操作:若將圖1中的△C′DE,繞點(diǎn)C按順時針方向任意旋轉(zhuǎn)一個角度α,連接AD,BE,如圖3;在圖3中,線段BE與AD之間具有怎樣的大小關(guān)系?證明你的結(jié)論; 
猜想與發(fā)現(xiàn):
根據(jù)上面的操作過程,請你猜想當(dāng)α為多少度時,線段AD的長度最大是多少?當(dāng)α為多少度時,線段AD的長度最小是多少?
【答案】
(1)解:BE=AD.
∵△C′DE繞點(diǎn)C按順時針方向旋轉(zhuǎn)30°,
∴∠BCE=∠ACD=30度,
∵△ABC與△C′DE是等邊三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD
(2)解:BE=AD.
∵△C′DE繞點(diǎn)C按順時針方向旋轉(zhuǎn)的角度為α,
∴∠BCE=∠ACD=α,
∵△ABC與△C′DE是等邊三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD.
猜想與發(fā)現(xiàn):
當(dāng)α為180°時,線段AD的長度最大,等于a+b;當(dāng)α為0°(或360°)時,線段AD的長度最小,等于a﹣b
【解析】(1)根據(jù)旋轉(zhuǎn)的性質(zhì)及等邊三角形的性質(zhì),利用SAS判定△BCE≌△ACD,根據(jù)全等三角形的對應(yīng)邊相等,可得到BE=AD.(2)圍繞證明△BCE≌△ACD,根據(jù)SAS尋找全等的條件,方法不變.
【考點(diǎn)精析】關(guān)于本題考查的等邊三角形的性質(zhì)和旋轉(zhuǎn)的性質(zhì),需要了解等邊三角形的三個角都相等并且每個角都是60°;①旋轉(zhuǎn)后對應(yīng)的線段長短不變,旋轉(zhuǎn)角度大小不變;②旋轉(zhuǎn)后對應(yīng)的點(diǎn)到旋轉(zhuǎn)到旋轉(zhuǎn)中心的距離不變;③旋轉(zhuǎn)后物體或圖形不變,只是位置變了才能得出正確答案.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,某學(xué)生在旗桿EF與實(shí)驗(yàn)樓CD之間的A處,測得∠EAF=60°,然后向左移動10米到B處,測得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 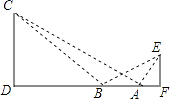
(1)求旗桿EF的高(結(jié)果保留根號);
(2)求旗桿EF與實(shí)驗(yàn)樓CD之間的水平距離DF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】希望中學(xué)開展以“我最喜歡的職業(yè)”為主題的調(diào)查活動,通過對學(xué)生的隨機(jī)抽樣調(diào)查得到一組數(shù)據(jù),如圖是根據(jù)這組數(shù)據(jù)繪制的不完整的統(tǒng)計(jì)圖,則下列說法中,不正確的是( )
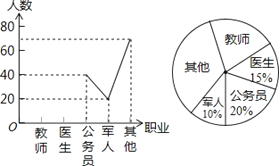
A. 被調(diào)查的學(xué)生有200人
B. 被調(diào)查的學(xué)生中喜歡教師職業(yè)的有40人
C. 被調(diào)查的學(xué)生中喜歡其他職業(yè)的占40%
D. 扇形圖中,公務(wù)員部分所對應(yīng)的圓心角為72°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
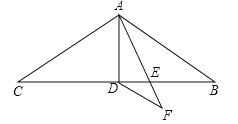
【題目】如圖在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中線,AE是∠BAD的角平分線,DF∥AB交AE的延長線于點(diǎn)F,求DF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,點(diǎn)M為直線AB上一動點(diǎn), ![]() 都是等邊三角形,連接BN
都是等邊三角形,連接BN
![]() 求證:
求證: ![]() ;
;
![]() 分別寫出點(diǎn)M在如圖2和圖3所示位置時,線段AB、BM、BN三者之間的數(shù)量關(guān)系
分別寫出點(diǎn)M在如圖2和圖3所示位置時,線段AB、BM、BN三者之間的數(shù)量關(guān)系![]() 不需證明
不需證明![]() ;
;
![]() 如圖4,當(dāng)
如圖4,當(dāng)![]() 時,證明:
時,證明: ![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
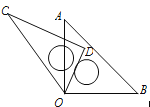
【題目】如圖所示,將一副直角三角板的頂點(diǎn)疊合在一起,記為點(diǎn)O(∠C=30°,∠A=45°).
(1)當(dāng)∠AOC=45°時,求∠DOB的度數(shù);
(2)請?zhí)骄俊?/span>AOC和∠DOB之間滿足的數(shù)量關(guān)系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知AC⊥BC,BD⊥AD,AC 與BD 交于O,AC=BD.
求證:(1)BC=AD;
(2)△OAB是等腰三角形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,AB=AC,點(diǎn)D是直線BC上一點(diǎn)(不與B、C重合),以AD為一邊在AD的右側(cè)作△ADE,使AD=AE,∠DAE=∠BAC,連接CE.
(1)如圖1,當(dāng)點(diǎn)D在線段BC上,如果∠BAC=90°,則∠BCE=_______度;
(2)如圖2如果∠BAC=60°,則∠BCE=______度;
(3)設(shè)∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
①如圖3,當(dāng)點(diǎn)D在線段BC上移動,則![]() 之間有怎樣的數(shù)量關(guān)系?請說明理由;
之間有怎樣的數(shù)量關(guān)系?請說明理由;
②當(dāng)點(diǎn)D在直線BC上移動,請直接寫出![]() 之樣的數(shù)量關(guān)系,不用證明。
之樣的數(shù)量關(guān)系,不用證明。




查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
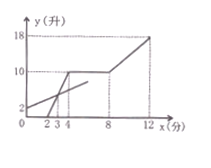
【題目】現(xiàn)有甲、乙兩個容器,分別裝有進(jìn)水管和出水管 ,兩容器的進(jìn)出水速度不變,先打開乙容器的進(jìn)水管,2分鐘時再打開甲容器的進(jìn)水管,又過2分鐘關(guān)閉甲容器的進(jìn)水管,再過4分鐘同時打開甲容器的進(jìn)、出水管。直到12分鐘時,同時關(guān)閉兩容器的進(jìn)出水管。打開和關(guān)閉水管的時間忽略不計(jì)。容器中的水量y(升)與乙容器注水時間x(分)之間的關(guān)系如圖所示
(1)求甲容器的進(jìn)、出水速度;
(2)當(dāng)![]() 時,在這過程中是否存在兩容器的水量相等?若存在,求出此時x的值;
時,在這過程中是否存在兩容器的水量相等?若存在,求出此時x的值;
(3)如果在乙容器中再裝一個進(jìn)水管,其進(jìn)水速度是2升/分,若使兩容器第12分鐘時的水量相等 ,則應(yīng)該在第幾分鐘打開此進(jìn)水管?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com