
【題目】如圖,在平面直角坐標系中,直線![]() 分別交x軸、y軸于點B,C,正方形AOCD的頂點D在第二象限內,E是BC中點,OF⊥DE于點F,連結OE,動點P在AO上從點A向終點O勻速運動,同時,動點Q在直線BC上從某點Q1向終點Q2勻速運動,它們同時到達終點.
分別交x軸、y軸于點B,C,正方形AOCD的頂點D在第二象限內,E是BC中點,OF⊥DE于點F,連結OE,動點P在AO上從點A向終點O勻速運動,同時,動點Q在直線BC上從某點Q1向終點Q2勻速運動,它們同時到達終點.
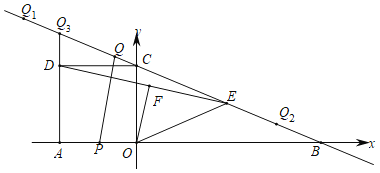
(1)求點B的坐標和OE的長;
(2)設點Q2為(m,n),當![]() tan∠EOF時,求點Q2的坐標;
tan∠EOF時,求點Q2的坐標;
(3)根據(2)的條件,當點P運動到AO中點時,點Q恰好與點C重合.
①延長AD交直線BC于點Q3,當點Q在線段Q2Q3上時,設Q3Q=s,AP=t,求s關于t的函數表達式.
②當PQ與△OEF的一邊平行時,求所有滿足條件的AP的長.
【答案】(1)(8,0),![]() ;(2)(6,1);(3)①
;(2)(6,1);(3)①![]() ,②
,②![]() 的長為
的長為![]() 或
或![]() .
.
【解析】
(1)令y=0,可得B的坐標,利用勾股定理可得BC的長,即可得到OE;
(2)如圖,作輔助線,證明△CDN∽△MEN,得CN=MN=1,計算EN的長,根據面積法可得OF的長,利用勾股定理得OF的長,由![]() 和
和![]() ,可得結論;
,可得結論;
(3)①先設s關于t成一次函數關系,設s=kt+b,根據當點P運動到AO中點時,點Q恰好與點C重合,得t=2時,CD=4,DQ3=2,s=![]() ,根據Q3(4,6),Q2(6,1),可得t=4時,s=
,根據Q3(4,6),Q2(6,1),可得t=4時,s=![]() ,利用待定系數法可得s關于t的函數表達式;
,利用待定系數法可得s關于t的函數表達式;
②分三種情況:
(i)當PQ∥OE時,根據![]() ,表示BH的長,根據AB=12,列方程可得t的值;
,表示BH的長,根據AB=12,列方程可得t的值;
(ii)當PQ∥OF時,根據tan∠HPQ=tan∠CDN=![]() ,列方程為2t2=
,列方程為2t2=![]() (7
(7![]() t),可得t的值.
t),可得t的值.
(iii)由圖形可知PQ不可能與EF平行.
解:(1)令![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() 為
為![]() .
.
∵![]()
![]() ,
,
在![]() 中,
中,![]() .
.
又∵![]() 為
為![]() 中點,∴
中點,∴![]() .
.
(2)如圖,作![]() 于點
于點![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
由勾股定理得![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 為
為![]() .
.

(3)①∵動點![]() 同時作勻速直線運動,
同時作勻速直線運動,
∴![]() 關于
關于![]() 成一次函數關系,設
成一次函數關系,設![]() ,
,
將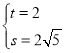 和
和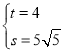 代入得
代入得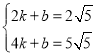 ,解得
,解得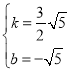 ,
,
∴![]() .
.
②(ⅰ)當![]() 時,(如圖),
時,(如圖),![]() ,
,
作![]() 軸于點
軸于點![]() ,則
,則![]() .
.
∵![]()
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
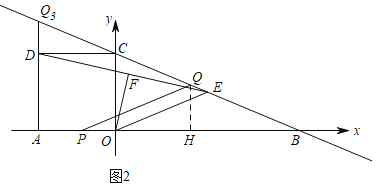
(ⅱ)當![]() 時(如圖),過點
時(如圖),過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,由
,由![]() 得
得![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(ⅲ)由圖形可知![]() 不可能與
不可能與![]() 平行.
平行.
綜上所述,當![]() 與
與![]() 的一邊平行時,
的一邊平行時,![]() 的長為
的長為![]() 或
或![]() .
.


 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:
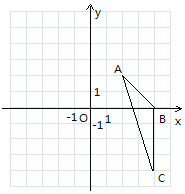
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別為A(2,2),B(4,0),C(4,-4).
(1)請在圖中畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(2)以點O為位似中心,將△ABC縮小為原來的![]() ,得到△A2B2C2,請在圖中y軸右側畫出△A2B2C2,;
,得到△A2B2C2,請在圖中y軸右側畫出△A2B2C2,;
(3)填空:△AA1A2的面積為________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
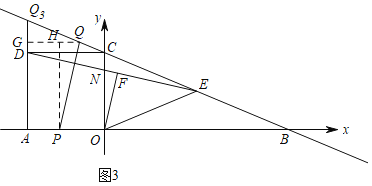
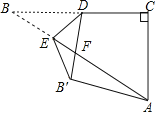
【題目】如圖,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,點D是BC的中點,點E是邊AB上一動點,沿DE所在直線把△BDE翻折到△B′DE的位置,B′D交AB于點F.若△AB′F為直角三角形,則AE的長為_____.
,AC=2,點D是BC的中點,點E是邊AB上一動點,沿DE所在直線把△BDE翻折到△B′DE的位置,B′D交AB于點F.若△AB′F為直角三角形,則AE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(發現問題)愛好數學的小明在做作業時碰到這樣的一道題目:
如圖①,點O為坐標原點,⊙O的半徑為1,點A(2,0).動點B在⊙O上,連結AB,作等邊△ABC(A,B,C為順時針順序),求OC的最大值
(解決問題)小明經過多次的嘗試與探索,終于得到解題思路:在圖①中,連接OB,以OB為邊在OB的左側作等邊三角形BOE,連接AE.
(1)請你找出圖中與OC相等的線段,并說明理由;
(2)求線段OC的最大值.
(靈活運用)
(3)如圖②,在平面直角坐標系中,點A的坐標為(2,0),點B的坐標為(5,0),點P為線段AB外一動點,且PA=2,PM=PB,∠BPM=90°,求線段AM長的最大值及此時點P的坐標.
(遷移拓展)
(4)如圖③,BC=4![]() ,點D是以BC為直徑的半圓上不同于B、C的一個動點,以BD為邊作等邊△ABD,請直接寫出AC的最值.
,點D是以BC為直徑的半圓上不同于B、C的一個動點,以BD為邊作等邊△ABD,請直接寫出AC的最值.

查看答案和解析>>
科目:初中數學 來源: 題型:
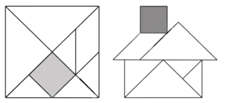
【題目】“七巧板”是我們祖先的一項卓越創造,可以拼出許多有趣的圖形,被譽為“東方魔板”,圖①是由邊長![]() 的正方形薄板分成7塊制作成的“七巧板”圖②是用該“七巧板”拼成的一個“家”的圖形,該“七巧板”中7塊圖形之一的正方形邊長為_______
的正方形薄板分成7塊制作成的“七巧板”圖②是用該“七巧板”拼成的一個“家”的圖形,該“七巧板”中7塊圖形之一的正方形邊長為_______![]() (結果保留根號).
(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
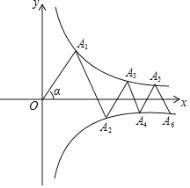
【題目】如圖,點A1、A3、A5…在反比例函數y=![]() (x>0)的圖象上,點A2、A4、A6……在反比例函數y=-
(x>0)的圖象上,點A2、A4、A6……在反比例函數y=-![]() (x>0)的圖象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,則An(n為正整數)的縱坐標為________________________________.(用含n的式子表示)
(x>0)的圖象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,則An(n為正整數)的縱坐標為________________________________.(用含n的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
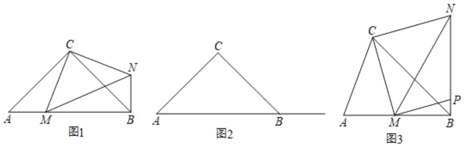
【題目】在△ABC中,∠ABC為銳角,點M為射線AB上一動點,連接CM,以點C為直角頂點,以CM為直角邊在CM右側作等腰直角三角形CMN,連接NB.
(1)如圖1,圖2,若△ABC為等腰直角三角形,
問題初現:①當點M為線段AB上不與點A重合的一個動點,則線段BN,AM之間的位置關系是 ,數量關系是 ;
深入探究:②當點M在線段AB的延長線上時,判斷線段BN,AM之間的位置關系和數量關系,并說明理由;
(2)如圖3,∠ACB≠90°,若當點M為線段AB上不與點A重合的一個動點,MP⊥CM交線段BN于點P,且∠CBA=45°,BC=![]() ,當BM= 時,BP的最大值為 .
,當BM= 時,BP的最大值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
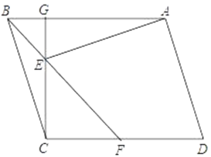
【題目】如圖,在ABCD中,CG⊥AB于點G,∠ABF=45°,F在CD上,BF交CG于點E,連接AE,且AE⊥AD.
(1)若BG=2,BC=![]() ,求EF的長度;
,求EF的長度;
(2)求證:CE+![]() BE=AB.
BE=AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校共有200名學生,為了解本學期學生參加公益勞動的情況,收集了他們參加公益勞動時間(單位:小時)等數據,以下是根據數據繪制的統計圖表的一部分.
學 生 類 型 人數 時間 |
|
|
|
|
| |
性別 | 男 | 7 | 31 | 25 | 30 | 4 |
女 | 8 | 29 | 26 | 32 | 8 | |
學段 | 初中 | 25 | 36 | 44 | 11 | |
高中 | ||||||

下面有四個推斷:
①這200名學生參加公益勞動時間的平均數一定在24.5-25.5之間
②這200名學生參加公益勞動時間的中位數在20-30之間
③這200名學生中的初中生參加公益勞動時間的中位數一定在20-30之間
④這200名學生中的高中生參加公益勞動時間的中位數可能在20-30之間
所有合理推斷的序號是( )
A. ①③B. ②④C. ①②③D. ①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com