
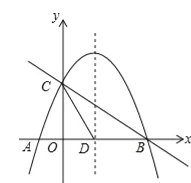
【題目】如圖,拋物線y=﹣![]() x2+bx+c與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
x2+bx+c與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
(1)求拋物線的解析式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,直接寫出P點的坐標;如果不存在,請說明理由;
(3)點E時線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時,△CBF的面積最大?求出△CBF的最大面積及此時E點的坐標.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2(2)存在,
x+2(2)存在,![]() 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )(3)4,E(2,1)
)(3)4,E(2,1)
【解析】
試題分析:(1)把A(﹣1,0),C(0,2)代入y=﹣![]() x2+bx+c列方程組即可.
x2+bx+c列方程組即可.
(2)先求出CD的長,分兩種情形①當CP=CD時,②當DC=DP時分別求解即可.
(3)求出直線BC的解析式,設E![]() ,則F
,則F![]() ,構建二次函數,利用二次函數的性質即可解決問題.
,構建二次函數,利用二次函數的性質即可解決問題.
試題解析:(1)把A(﹣1,0),C(0,2)代入y=﹣![]() x2+bx+c得
x2+bx+c得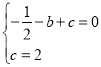 ,
,
解得b=![]() ,c=2,
,c=2,
∴拋物線的解析式為y=﹣![]() x2+
x2+![]() x+2.,
x+2.,
(2)存在.如圖1中,∵C(0,2),D(![]() ,0),
,0),
∴OC=2,OD=![]() ,CD=
,CD=![]() =
=![]()
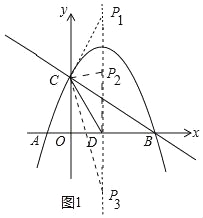
①當CP=CD時,可得P1(![]() ,4).
,4).
②當DC=DP時,可得P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )
)
綜上所述,滿足條件的P點的坐標為![]() 或(
或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
(3)如圖2中,
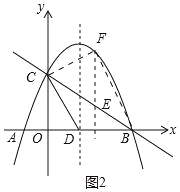
對于拋物線y=﹣![]() x2+
x2+![]() x+2,當y=0時,﹣
x+2,當y=0時,﹣![]() x2+
x2+![]() x+2=0,解得x1=4,x2=﹣1
x+2=0,解得x1=4,x2=﹣1
∴B(4,0),A(﹣1,0),
由B(4,0),C(0,2)得直線BC的解析式為y=﹣![]() x+2,
x+2,
設E![]() 則F
則F![]() ,
,
EF=![]() ﹣
﹣![]() =
=![]()
∴-![]() <0,∴當m=2時,EF有最大值2,
<0,∴當m=2時,EF有最大值2,
此時E是BC中點,
∴當E運動到BC的中點時,△EBC面積最大,
∴△EBC最大面積=![]() ×4×EF=
×4×EF=![]() ×4×2=4,此時E(2,1).
×4×2=4,此時E(2,1).


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:
【題目】下列事件中,必然事件是( )
A.拋擲1個均勻的骰子,出現6點向上
B.兩直線被第三條直線所截,同位角相等
C.366人中至少有2人的生日相同
D.實數的絕對值是非負數
查看答案和解析>>
科目:初中數學 來源: 題型:
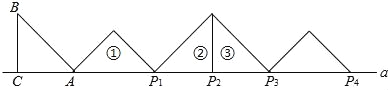
【題目】如圖,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC邊在直線a上,將△ABC繞點A順時針旋轉到位置①可得到點P1,此時AP1=![]() ;將位置①的三角形繞點P1順時針旋轉到位置②可得到點P2,此時AP2=
;將位置①的三角形繞點P1順時針旋轉到位置②可得到點P2,此時AP2=![]() +1;將位置②的三角形繞點P2順時針旋轉到位置③可得到點P3時,AP3=
+1;將位置②的三角形繞點P2順時針旋轉到位置③可得到點P3時,AP3=![]() +2…按此規律繼續旋轉,直至得到點P2026為止,則AP2016= .
+2…按此規律繼續旋轉,直至得到點P2026為止,則AP2016= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD⊥BC,EF垂直平分AC,交AC于點F,交BC于點E,且BD=DE.
⑴若∠BAE=40°,求∠C的度數;
⑵若△ABC周長13cm,AC=6cm,求DC長.

查看答案和解析>>
科目:初中數學 來源: 題型:
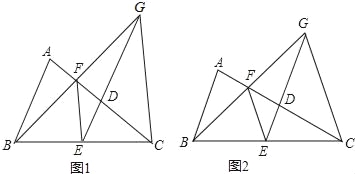
【題目】如圖,已知等腰△ABC中,AC=BC,點D、E、F分別是線段AC、BC、AD的中點,連接FE、ED,BF的延長線交ED的延長線于點G,連接GC.
(1)求證:EF∥CG;
(2)若AC=![]() AB,求證:AC=CG;
AB,求證:AC=CG;
(3)如圖2,若CG=EG,則![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
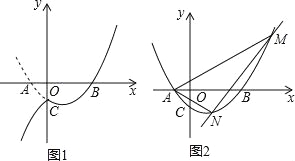
【題目】已知拋物線y=(m﹣1)x2+(m﹣2)x﹣1與x軸交于A、B兩點,若m>1,且點A在點B的左側,OA:OB=1:3
(1)試確定拋物線的解析式;
(2)直線y=kx﹣3與拋物線交于M、N兩點,若△AMN的內心在x軸上,求k的值.
(3)設(2)中拋物線與y軸的交點為C,過點C作直線l∥x軸,將拋物線在y軸左側的部分沿直線l翻折,拋物線的其余部分保持不變,得到一個新圖象,請你結合新圖象回答:當直線y=![]() x+b與新圖象只有一個公共點P(x0,y0)且y0≤7時,求b的取值范圍.
x+b與新圖象只有一個公共點P(x0,y0)且y0≤7時,求b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com