
【題目】如圖,在△ABC中,BD⊥AC,垂足為C,且∠A<∠C,點E是一動點,其在BC上移動,連接DE,并過點E作EF⊥DE,點F在AB的延長線上,連接DF交BC于點G.
(1)請同學們根據以上提示,在上圖基礎上補全示意圖.
(2)當△ABD與△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度數.
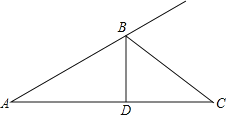
【答案】(1)詳見解析;(2)40°.
【解析】
(1)根據垂直畫出圖形即可得出結論;
(2)先根據兩三角形全等,判斷出AB=DF,進而判斷出BD=DE,再求出∠FDE=60°,進而利用三角形的外角的性質求出∠BDE=80°,進而求出∠DBE=∠BED=50°,即可得出結論.
(1)補全示意圖如圖所示,
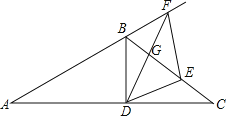
(2)∵DE⊥EF,BD⊥AC,
∴∠DEF=∠ADB=90°.
∵△ABD與△DEF全等,
∴AB=DF,
又∵AD=FE,
∴∠ABD=∠FDE,
∴BD=DE.
在Rt△ABD中,∠ABD=90°﹣∠A=60°.
∴∠FDE=60°.
∵∠ABD=∠BDF+∠AFD,
∵∠AFD=40°,
∴∠BDF=20°.
∴∠BDE=∠BDF+∠FDE=20°+60°=80°.
∵BD=DE,
∴∠DBE=∠BED=![]() (180°﹣∠BDE)=50°.
(180°﹣∠BDE)=50°.
在Rt△BDC中,∠C=90°﹣∠DBE=90°﹣50°=40°.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】某數學興趣小組在本校九年級學生中以“你最喜歡的項體育運動"為主體進行了抽樣調查,并將調查結果繪制成下表和下圖.
項目 | 籃球 | 乒乓球 | 羽毛球 | 跳繩 | 其他 |
人數 |
| 12 | 10 | 5 | 8 |

請根據圖表中的信息完成下列各題:
(1)本次共調查學生______名;
(2)![]() =______;
=______;
(3)在扇形圖中,“跳繩”對應的扇形圓是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 網格中,每個小正方形的邊長都為
網格中,每個小正方形的邊長都為![]() .
.
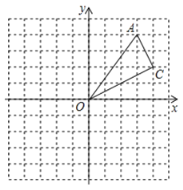
(1)建立如圖所示的平面直角坐標系,若點![]() ,則點
,則點![]() 的坐標_______________;
的坐標_______________;
(2)將![]() 向左平移
向左平移![]() 個單位,向上平移
個單位,向上平移![]() 個單位,則點
個單位,則點![]() 的坐標變為_____________;
的坐標變為_____________;
(3)若將![]() 的三個頂點的橫縱坐標都乘以
的三個頂點的橫縱坐標都乘以![]() ,請畫出
,請畫出![]() ;
;
(4)圖中格點![]() 的面積是_________________;
的面積是_________________;
(5)在![]() 軸上找一點
軸上找一點![]() ,使得
,使得![]() 最小,請畫出點
最小,請畫出點![]() 的位置,并直接寫出
的位置,并直接寫出![]() 的最小值是______________.
的最小值是______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=9,AC=6,BC=12,點M在AB邊上,且AM=3,過點M作直線MN與AC邊交于點N,使截得的三角形與原三角形相似,則MN=__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,矩形
,矩形![]() 的一邊落在矩形
的一邊落在矩形![]() 的一邊上,并且矩形
的一邊上,并且矩形![]() ,其相似比為
,其相似比為![]() ,連接
,連接![]() 、
、![]() .
.

![]() 試探究
試探究![]() 、
、![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
![]() 將矩形
將矩形![]() 繞著點
繞著點![]() 按順時針(或逆時針)旋轉任意角度
按順時針(或逆時針)旋轉任意角度![]() ,得到圖形
,得到圖形![]() 、圖形
、圖形![]() ,請你通過觀察、分析、判斷
,請你通過觀察、分析、判斷![]() 中得到的結論是否能成立,并選取圖
中得到的結論是否能成立,并選取圖![]() 證明你的判斷;
證明你的判斷;
![]() 在
在![]() 中,矩形
中,矩形![]() 繞著點
繞著點![]() 旋轉過程中,連接
旋轉過程中,連接![]() 、
、![]() 、
、![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 的面積是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,請說明理由.
的面積是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加強校園文化建設,某校準備打造校園文化墻,需用甲、乙兩種石材經市場調查,甲種石材的費用![]() (元)與使用面積
(元)與使用面積![]()
![]() 間的函數關系如圖所示,乙種石材的價格為每平方米
間的函數關系如圖所示,乙種石材的價格為每平方米![]() 元.
元.

(1)求![]() 與
與![]() 間的函數解析式;
間的函數解析式;
(2)若校園文化墻總面積共![]() ,其中使用甲石材
,其中使用甲石材![]()
![]() ,設購買兩種石材的總費用為
,設購買兩種石材的總費用為![]() 元,請直接寫出
元,請直接寫出![]() 與
與![]() 間的函數解析式;
間的函數解析式;
(3)在(2)的前提下,若甲種石材使用面積多于![]() ,且不超過乙種石材面積的
,且不超過乙種石材面積的![]() 倍,那么應該怎樣分配甲、乙兩種石材的面積才能使總費用最少?最少總費用為多少元?
倍,那么應該怎樣分配甲、乙兩種石材的面積才能使總費用最少?最少總費用為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).

(1)請畫出△ABC向左平移5個單位長度后得到的△A1B1C1;
(2)請畫出△ABC關于原點對稱的△A2B2C2;
(3)在x軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com