
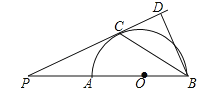
【題目】如圖,AB是半圓O的直徑,點P是BA延長線上一點,PC是⊙O的切線,切點為C,過點B作BD⊥PC交PC的延長線于點D,連接BC.求證:
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
試題分析:(1)連接OC,由PC為圓O的切線,利用切線的性質得到OC垂直于PC,再由BD垂直于PD,得到一對直角相等,利用同位角相等兩直線平行得到OC與BD平行,進而得到一對內錯角相等,再由OB=OC,利用等邊對等角得到一對角相等,等量代換即可得證;
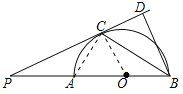
(2)連接AC,由AB為圓O的直徑,利用圓周角定理得到∠ACB為直角,利用兩對角相等的三角形相似得到三角形ABC與三角形CBD相似,利用相似三角形對應邊成比例,變形即可得證.
試題解析:(1)連接OC,∵PC與圓O相切,∴OC⊥PC,即∠OCP=90°,∵BD⊥PD,∴∠BDP=90°,∴∠OCP=∠PDB,∴OC∥BD,∴∠BCO=∠CBD,∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD;
(2)連接AC,∵AB為圓O的直徑,∴∠ACB=90°,∴∠ACB=∠CDB=90°,∵∠ABC=∠CBD,∴△ABC∽△CBD,∴![]() ,則
,則![]() =ABBD.
=ABBD.


科目:初中數學 來源: 題型:
【題目】某商場計劃采購甲、乙、丙三種型號的“格力”牌空調共25臺.三種型號的空調進價和售價如下表:
種類價格 | 甲 | 乙 | 丙 |
進價(元/臺) | 1600 | 1800 | 2400 |
售價(元/臺) | 1800 | 2050 | 2600 |
商場計劃投入總資金5萬元,所購進的甲、丙型號空調數量相同,乙型號數量不超過甲型號數量的一半.若設購買甲型號空調x臺,所有型號空調全部售出后獲得的總利潤為W元.
(1)求W與x之間的函數關系式.
(2)商場如何采購空調才能獲得最大利潤?
(3)由于原材料上漲,商場決定將丙型號空調的售價提高a元(a≥100),其余型號售價不變,則商場又該如何采購才能獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E,F,G,H分別是邊AB,BC,CD,DA的中點.
(1)判斷四邊形EFGH的形狀,并證明你的結論;
(2)當BD,AC滿足什么條件時,四邊形EFGH是正方形.(不要求證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】看過電視劇《西游記》的同學,一定很喜歡孫悟空,孫悟空的金箍棒能隨意伸縮,假設它最短時只有1厘米,第1次變化后變成3厘米,第2次變化后變成9厘米,第3次變化后變成27厘米……照此規律變化下去,到第5次變化后金箍棒的長是________米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有理數的乘方:求n個________因數的積的運算,叫做乘方,乘方的結果叫做________.在an中,a叫做________,n叫做________,讀作________或________;表示的意義為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】具有綠色低碳、方便快捷、經濟環保等特點的共享單車行業近幾年蓬勃發展,我國2017年全年共享單車用戶達6170萬人.將數據“6170萬”用科學記數法表示為( )
A. 6.17×103 B. 6.17×105 C. 6.17×107 D. 6.17×109
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,假命題是( )
A. 鄰補角的平分線互相垂直
B. 平行于同一直線的兩條直線互相平行
C. 垂直于同一直線的兩條直線互相垂直
D. 平行線的一組內錯角的平分線互相平行
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com