【題目】某商家在購進一款產品時，由于運輸成本及產品成本的提高，該產品第 x 天的成本 y（元/件）與 x（天）之間的關系如圖所示，并連續 60 天均以 80 元/件的價格出售， 第 x 天該產品的銷售量 z（件）與 x（天）滿足關系式 z＝x+15．
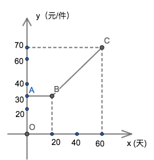
（1）第 25 天，該商家的成本是 元，獲得的利潤是 元；
（2）設第 x 天該商家出售該產品的利潤為 w 元．
①求 w 與 x 之間的函數關系式；
②求出第幾天的利潤最大，最大利潤是多少？
【答案】（1）35，1800；（2）①
；②第27或28天的利潤最大，最大為1806元．
【解析】
（1）根據已知條件可知第25天時的成本為35元，此時的銷售量為40，則可求得第25天的利潤．
（2）①利用每件利潤×總銷量＝總利潤，分當0＜x≤20時與20＜x≤60時，分別列出函數關系式；
②利用一次函數及二次函數的性質即可解答．
解：（1）由圖象可知，此時的銷售量為z＝25＋15＝40（件），
設直線BC的關系為y＝kx＋b，將B（20,30）、C（60,70）代入
得：
，解得：k=1，b=10，
∴y＝x＋10，
∴第 25 天，該商家的成本是y=25+10=35（元）
則第25天的利潤為：（8035）×40＝1800（元）；
故答案為：35，1800；
（2）①當0＜x≤20時，
；
當20＜x≤60時，
，
∴
②當0＜x≤20時，∵50＞0，w隨x的增大而增大，
∴當x=20時，w=50×20+750=1750（元），
當20＜x≤60時，
，
∵-1＜0，拋物線開口向下，對稱軸為
，
當x=27與x=28時，
（元）
∵1806＞1750，
∴第27或28天的利潤最大，最大為1806元．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】在一個不透明的口袋里裝有分別標有數字-3、-1、0、2的四個小球，除數字不同外，小球沒有任何區別，每次試驗先攪拌均勻．
（1）從中任取一球，將球上的數字記為a，則關于x的元二次方程x2-2x-a+1=0有實數根的概率______；
（2）從中任取一球，將球上的數字作為點的橫坐標，記為x（不放回）；再任取一球，將球上的數字作為點的縱坐標，記為y，試用畫樹狀圖（或列表法）表示出點（x，y）所有可能出現的結果，并求點（x，y）落在第三象限內的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為實現區域教育均衡發展，我市計劃對某縣A、B兩類薄弱學校全部進行改造．根據預算，共需資金1555萬元改造一所A類學校和兩所B類學校共需資金230萬元；改造兩所A類學校和一所B類學校共需資金205萬元
（1）改造一所A類學校和一所B類學校所需的資金分別是多少萬元？
（2）根據我市教育局規劃計劃今年對該縣A、B兩類學校進行改造，要求改造的A類學校是B類學校的2倍多2所，在計劃投入資金不超過1555萬元的條件下，至多能改造多少所A類學校？
查看答案和解析>>
科目：初中數學 來源： 題型：
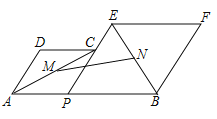
【題目】如圖，已知
，
為線段
上的一個動點，分別以
，
為邊在的同側作菱形
和菱形
．點，
，
在一條直線上，
，
、
分別是對角線
、
的中點．當點在線段上移動時，點、之間的距離最短為_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有四個外觀與質地完全相同的小球，小球上分別標有數字
．將四個小球放置于不透明的盒子中，搖勻后，甲從中隨機抽取一個小球，記錄數字后放回搖勻，乙再隨機抽取一個．
（1）請用列表法或畫樹狀圖的方法，求兩人抽取相同數字的概率．
（2）若兩人抽取的數字和為
的倍數，則甲獲勝；若抽取的數字和為
的倍數，則乙獲勝，否則為平局．這個游戲公平嗎？請用所學的概率的知識加以解釋．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校餐廳中，一張桌子可坐6人，現有以下兩種擺放方式:
（1）當有5張桌子時，第一種方式能坐 人，第二種方式能坐 人．
（2）當有n張桌子時，第一種方式能坐 人，第二種方式能坐 人．
（3）新學期有200人在學校就餐，但餐廳只有60張這樣的餐桌，若你是老師，你打算選擇以下哪種方式來擺放餐桌?為什么?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：點P是△ABC內部或邊上的點（頂點除外），在△PAB，△PBC，△PCA中，若至少有一個三角形與△ABC相似，則稱點P是△ABC的自相似點．
例如：如圖1，點P在△ABC的內部，∠PBC=∠A，∠PCB=∠ABC，則△BCP∽△ABC，故點P為△ABC的自相似點．
請你運用所學知識，結合上述材料，解決下列問題：
在平面直角坐標系中，點M是曲線C：
上的任意一點，點N是x軸正半軸上的任意一點．
（1） 如圖2，點P是OM上一點，∠ONP=∠M, 試說明點P是△MON的自相似點； 當點M的坐標是
，點N的坐標是
時，求點P 的坐標；
（2） 如圖3，當點M的坐標是
，點N的坐標是
時，求△MON的自相似點的坐標；
（3） 是否存在點M和點N,使△MON無自相似點,？若存在，請直接寫出這兩點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場用36000元購進甲、乙兩種商品，銷售完后共獲利6000元．其中甲種商品每件進價120元，售價138元；乙種商品每件進價100元，售價120元．
（1）該商場購進甲、乙兩種商品各多少件？
（2）商場第二次以原進價購進甲、乙兩種商品，購進乙種商品的件數不變，而購進甲種商品的件數是第一次的2倍，甲種商品按原售價出售，而乙種商品打折銷售．若兩種商品銷售完畢，要使第二次經營活動獲利不少于8160元，乙種商品最低售價為每件多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
