
【題目】為節約用水,某市居民生活用水按階梯式水價計量,水價分為三個階梯,價格表如下表所示:
某市自來水銷售價格表
類別 | 月用水量 (立方米) | 供水價格 (元/立方米) | 污水處理費 (元/立方米) | |
居民生活用水 | 階梯一 | 0~18(含18) | 1.90 | 1.00 |
階梯二 | 18~25(含25) | 2.85 | ||
階梯三 | 25以上 | 5.70 | ||
(注:居民生活用水水價=供水價格+污水處理費)
(1)當居民月用水量在18立方米及以下時,水價是_____元/立方米.
(2)4月份小明家用水量為20立方米,應付水費為:
18×(1.90+1.00)+2×(2.85+1.00)=59.90(元)
預計6月份小明家的用水量將達到30立方米,請計算小明家6月份的水費.
(3)為了節省開支,小明家決定每月用水的費用不超過家庭收入的1%,已知小明家的平均月收入為7530元,請你為小明家每月用水量提出建議
【答案】(1)1.90;(2)112.65元;(3)當小明家每月的用水量不要超過24立方米時,水費就不會超過他們家庭總收入的1%.
【解析】
試題
(1)由表中數據可知,當用水量在18立方米及以下時,水價為1.9元/立方米;
(2)由題意可知小明家6月份的水費是:(1.9+1)×18+(2.85+1)×7+(5.70+1)×5=112.65(元);
(3)由已知條件可知,用水量為18立方米時,應交水費52.2元,當用水量為25立方米時,應交水費79.15元,而小明家計劃的水費不超過75.3元,由此可知他們家的用水量不會超過25立方米,設他們家的用水量為x立方米,則由題意可得:18×(1.9+1)+(x-18)×(2.85+1)![]() 75.3,解得:x
75.3,解得:x![]() 24,即小明家每月的用水量不要超過24立方米.
24,即小明家每月的用水量不要超過24立方米.
試題解析:
(1)由表中數據可知,當用水量在18立方米及以下時,水價為1.9元/立方米;
(2)由題意可得:
小明家6月份的水費是:(1.9+1)×18+(2.85+1)×7+(5.70+1)×5=112.65(元);
(3)由題意可知,當用水量為18立方米時,應交水費52.2元,當用水量為25立方米時,應交水費79.15元,而小明家計劃的水費不超過75.3元,由此可知他們家的用水量不超過18立方米,而不足25立方米,設他們家的用水量為x立方米,則由題意可得:
18×(1.9+1)+(x-18)×(2.85+1)![]() 75.3,解得:x
75.3,解得:x![]() 24,
24,
∴當小明家每月的用水量不要超過24立方米時,水費就不會超過他們家庭總收入的1%.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優沖刺100分系列答案
全優沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸,y軸分別交于B,C兩點,拋物線
與x軸,y軸分別交于B,C兩點,拋物線![]() 過點B,C.
過點B,C.
(1)求b、c的值;
(2)若點D是拋物線在x軸下方圖象上的動點,過點D作x軸的垂線,與直線BC相交于點E.當線段DE的長度最大時,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是它的角平分線,G是AD上的一點,BG,CG分別平分∠ABC,∠ACB,GH⊥BC,垂足為H,

求證:(1)∠BGC=90°+![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
查看答案和解析>>
科目:初中數學 來源: 題型:
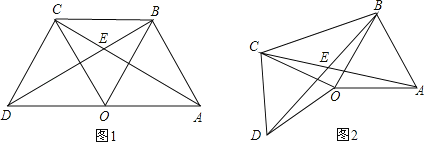
【題目】(1)如圖1,點O是線段AD的中點,分別以AO和DO為邊在線段AD的同側作等邊三角形OAB和等邊三角形OCD,連接AC和BD,相交于點E,連接BC.求∠AEB的大小;
(2)如圖2,△OAB固定不動,保持△OCD的形狀和大小不變,將△OCD繞點O旋轉(△OAB和△OCD不能重疊),求∠AEB的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小莉和她爸爸兩人沿長江邊揚子江步道勻速跑步,他們從渡江勝利紀念館同時出發,終點是綠博園.已知小莉比她爸爸每步少跑![]() ,兩人的運動手環記錄時間和步數如下:
,兩人的運動手環記錄時間和步數如下:
出發 | 途中 | 結束 | |
時間 |
|
|
|
小莉的步數 | 1308 | 3183 | 8808 |
出發 | 途中 | 結束 | |
時間 |
|
|
|
爸爸的步數 | 2168 | 4168 |
|
(1)表格中![]() 表示的結束時間為 ,
表示的結束時間為 ,![]() ;
;
(2)小莉和她爸爸兩人每步分別跑多少米?
(3)渡江勝利紀念館到綠博園的路程是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
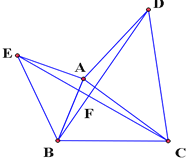
【題目】如圖,已知△ABC,分別以AB,AC為直角邊,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,連結BD,CE交于點F,設AB=m,BC=n.
(1)求證:∠BDA=∠ECA.
(2)若m=![]() ,n=3,∠ABC=75°,求BD的長.
,n=3,∠ABC=75°,求BD的長.
(3)當∠ABC=____時,BD最大,最大值為____(用含m,n的代數式表示)
(4)試探究線段BF,AE,EF三者之間的數量關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別是A(2,2),B(4,0),C(4,﹣4).
(1)請在圖中,畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(2)以點O為位似中心,將△ABC縮小為原來的![]() ,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() 的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
(1)求一次函數y=kx+b和y=![]() 的表達式;
的表達式;
(2)已知點C在x軸上,且△ABC的面積是8,求此時點C的坐標;
(3)反比例函數y=![]() (1≤x≤4)的圖象記為曲線C1,將C1向右平移3個單位長度,得曲線C2,則C1平移至C2處所掃過的面積是_________.(直接寫出答案)
(1≤x≤4)的圖象記為曲線C1,將C1向右平移3個單位長度,得曲線C2,則C1平移至C2處所掃過的面積是_________.(直接寫出答案)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC內一點D,點C是AE上一點,AD交BE于點P,射線DC交BE的延長線于點F,且∠ABD=∠ACD,∠PDB=∠PDC
(1)求證:AB=AC;
(2)若AB=3,AE=5,求![]() 的值;
的值;
(3)若![]() ,
,![]() =m,則
=m,則![]() =_______.
=_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com