
【題目】已知,在![]() 中,
中,![]() ,
,![]() 為
為![]() 上一動(dòng)點(diǎn),以
上一動(dòng)點(diǎn),以![]() 為斜邊作
為斜邊作![]() ,
,![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() .
.
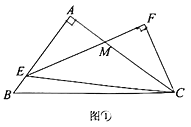
(1)如圖①,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的長(zhǎng)
的長(zhǎng)
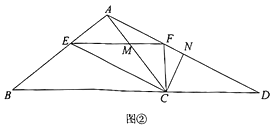
(2)如圖②,連接![]() 并延長(zhǎng)交
并延長(zhǎng)交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 于
于![]() ,求證
,求證![]() .
.
【答案】(1)12;(2)見(jiàn)解析
【解析】
(1)由“SAS”可證△AEM≌△FCM,可得EM=MC,由等腰三角形性質(zhì)可求∠AEF=∠MCE=∠MEC=30°,由直角三角形的性質(zhì)可求ME=MC=8,即可求AC的長(zhǎng);
(2)過(guò)點(diǎn)C作CG⊥AC交AD于點(diǎn)G,由“SAS”可證△ACG≌△EFC,可得AG=CE,CF=CG,由等腰三角形的性質(zhì)可得FG=2FN,即可得結(jié)論.
(1)∵EF平分∠AEC,
∴∠AEF=∠FEC,
∵∠BAC=∠EFC=90°,AM=MF,∠AME=∠FMC
∴△AEM≌△FCM(SAS)
∴EM=MC
∴∠MEC=∠MCE
∴∠MEC=∠MCE=∠AEF,
∵∠MEC+∠MCE+∠AEF=90°
∴∠AEF=∠MCE=∠MEC=30°,且∠BAC=90°
∴EM=2AM=8
∴MC=8
∴AC=AM+MC=12
(2)如圖,過(guò)點(diǎn)C作CG⊥AC交AD于點(diǎn)G,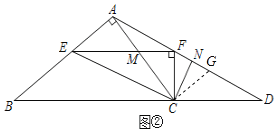
由(1)可知:EM=MC
∵AM=MF
∴AC=EF,
∵∠BAC=∠EFC=90°
∴點(diǎn)A,點(diǎn)F,點(diǎn)C,點(diǎn)E四點(diǎn)共圓
∴∠CAG=∠FEC,且AC=EF,∠EFC=∠ACG=90°
∴△ACG≌△EFC(ASA)
∴AG=CE,CF=CG,
∵CF=CG,CN⊥AG
∴FG=2FN
∴EC=AG=AF+FG=AF+2FN


 期末好成績(jī)系列答案
期末好成績(jī)系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在□ABCD中,AD=2AB,F是AD的中點(diǎn),作CE⊥AB,垂足E在線段AB上,連接EF、CF,則下列結(jié)論:(1)∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正確的結(jié)論是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正確的結(jié)論是( )
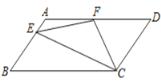
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀材料:小明在學(xué)習(xí)二次根式后,發(fā)現(xiàn)一些含根號(hào)的式子可以寫(xiě)成另一個(gè)式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明進(jìn)行了以下探索:
)2,善于思考的小明進(jìn)行了以下探索:
設(shè)a+b=(m+n![]() )2(其中a、b、m、n均為整數(shù)),則有a+b
)2(其中a、b、m、n均為整數(shù)),則有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.這樣小明就找到了一種把部分a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請(qǐng)你仿照小明的方法探索并解決下列問(wèn)題:
(1)當(dāng)a、b、m、n均為正整數(shù)時(shí),若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分別表示a、b,得a= ,b= ;
)2,用含m、n的式子分別表示a、b,得a= ,b= ;
(2)試著把7+4![]() 化成一個(gè)完全平方式.
化成一個(gè)完全平方式.
(3)若a是216的立方根,b是16的平方根,試計(jì)算:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知點(diǎn)![]() 分別在
分別在![]() 的邊
的邊![]() 上運(yùn)動(dòng)(不與點(diǎn)
上運(yùn)動(dòng)(不與點(diǎn)![]() 重合),
重合),![]() 是
是![]() 的平分線,
的平分線,![]() 的延長(zhǎng)線交角
的延長(zhǎng)線交角![]() 的平分線于點(diǎn)
的平分線于點(diǎn)![]() .
.

(1)若![]() ,求
,求![]() 的度數(shù).
的度數(shù).
(2)若![]() ,求
,求![]() 的度數(shù).
的度數(shù).
(3)若![]() ,請(qǐng)用含
,請(qǐng)用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在正方形ABCD中,BD是一條對(duì)角線,點(diǎn)E在直線CD上(與點(diǎn)C,D不重合),連接AE,平移△ADE,使點(diǎn)D移動(dòng)到點(diǎn)C,得到△BCF,過(guò)點(diǎn)F作FG⊥BD于點(diǎn)G,連接AG,EG.

(1)問(wèn)題猜想:如圖1,若點(diǎn)E在線段CD上,試猜想AG與EG的數(shù)量關(guān)系是____________,位置關(guān)系是____________;
(2)類(lèi)比探究:如圖2,若點(diǎn)E在線段CD的延長(zhǎng)線上,其余條件不變,小明猜想(1)中的結(jié)論仍然成立,請(qǐng)你給出證明;
(3)解決問(wèn)題:若點(diǎn)E在線段DC的延長(zhǎng)線上,且∠AGF=120°,正方形ABCD的邊長(zhǎng)為2,請(qǐng)?jiān)趥溆脠D中畫(huà)出圖形,并直接寫(xiě)出DE的長(zhǎng)度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知![]() 三個(gè)頂點(diǎn)的坐標(biāo)分別為
三個(gè)頂點(diǎn)的坐標(biāo)分別為![]() ,
,![]() ,
,![]() ,
,
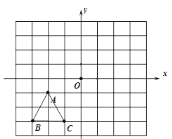
(1)若將△ABC 向右平移三個(gè)單位長(zhǎng)度得到△A1B1C1,則點(diǎn) A1 的坐標(biāo)為________![]()
(2)若△ABC 與△A2B2C2 關(guān)于原點(diǎn) O 成中心對(duì)稱(chēng),則點(diǎn) A2 的坐標(biāo)________;
(3)畫(huà)出△ABC 繞原點(diǎn) O 順時(shí)針旋轉(zhuǎn) 90°后的對(duì)應(yīng)圖形△A3B3C3,并寫(xiě)出 A3 的坐標(biāo)_____
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商城銷(xiāo)售A,B兩種自行車(chē).A型自行車(chē)售價(jià)為2 100元/輛,B型自行車(chē)售價(jià)為1 750元/輛,每輛A型自行車(chē)的進(jìn)價(jià)比每輛B型自行車(chē)的進(jìn)價(jià)多400元,商城用80 000元購(gòu)進(jìn)A型自行車(chē)的數(shù)量與用64 000元購(gòu)進(jìn)B型自行車(chē)的數(shù)量相等.
(1)求每輛A,B兩種自行車(chē)的進(jìn)價(jià)分別是多少?
(2)現(xiàn)在商城準(zhǔn)備一次購(gòu)進(jìn)這兩種自行車(chē)共100輛,設(shè)購(gòu)進(jìn)A型自行車(chē)m輛,這100輛自行車(chē)的銷(xiāo)售總利潤(rùn)為y元,要求購(gòu)進(jìn)B型自行車(chē)數(shù)量不超過(guò)A型自行車(chē)數(shù)量的2倍,總利潤(rùn)不低于13 000元,求獲利最大的方案以及最大利潤(rùn).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校準(zhǔn)備組織七年級(jí)400名學(xué)生參加北京夏令營(yíng),已知用3輛小客車(chē)和1輛大客車(chē)每次可運(yùn)送學(xué)生105人;用1輛小客車(chē)和2輛大客車(chē)每次可運(yùn)送學(xué)生110人;
(1)每輛小客車(chē)和每輛大客車(chē)各能坐多少名學(xué)生?
(2)若學(xué)校計(jì)劃租用小客車(chē)x輛,大客車(chē)y輛,一次送完,且恰好每輛車(chē)都坐滿(mǎn);
①請(qǐng)你設(shè)計(jì)出所有的租車(chē)方案;
②若小客車(chē)每輛需租金4000元,大客車(chē)每輛需租金7600元,請(qǐng)選出最省錢(qián)的租車(chē)方案,并求出最少租金.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AE=AC,AB=AD,∠EAB=∠CAD.
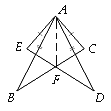
(1)BC與DE相等嗎?說(shuō)明理由.
(2)若BC與DE相交于點(diǎn)F,EF=CF.連接AF,∠BAF與∠DAF相等嗎?說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com