
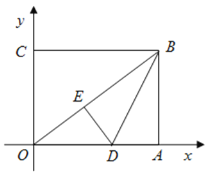
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點,矩形
為坐標原點,矩形![]() 的頂點
的頂點![]() 、
、![]() ,將矩形
,將矩形![]() 的一個角沿直線
的一個角沿直線![]() 折疊,使得點
折疊,使得點![]() 落在對角線
落在對角線![]() 上的點
上的點![]() 處,折痕與
處,折痕與![]() 軸交于點
軸交于點![]() .
.
(1)求線段![]() 的長度;
的長度;
(2)求直線![]() 所對應的函數表達式;
所對應的函數表達式;
(3)若點![]() 在線段
在線段![]() 上,在線段
上,在線段![]() 上是否存在點
上是否存在點![]() ,使以
,使以![]() 為頂點的四邊形是平行四邊形?若存在,請求出點
為頂點的四邊形是平行四邊形?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據勾股定理即可解決問題;
(2)設AD=x,則OD=OA=AD=12-x,根據軸對稱的性質,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根據OE2+DE2=OD2,構建方程即可解決問題;
(3)過點E作EP∥BD交BC于點P,過點P作PQ∥DE交BD于點Q,則四邊形DEPQ是平行四邊形,再過點E作EF⊥OD于點F,想辦法求出最小PE的解析式即可解決問題.
解:(1)由題知:![]() .
.
(2)設![]() ,則
,則![]() ,
,
根據軸對稱的性質,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得 ![]() ,
,
∴![]() ,
,
∴點![]() ,
,
設直線![]() 所對應的函數表達式為:
所對應的函數表達式為:![]() ,
,
則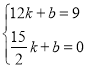 , 解得
, 解得![]() ,
,
∴直線![]() 所對應的函數表達式為:
所對應的函數表達式為:![]() ,
,
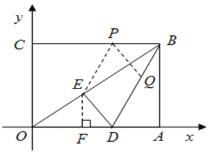
(3)存在,過點![]() 作EP∥DB交
作EP∥DB交![]() 于點
于點![]() ,過點
,過點![]() 作PQ∥ED交
作PQ∥ED交![]() 于點
于點![]() ,則四邊形
,則四邊形![]() 是平行四邊形.再過點
是平行四邊形.再過點![]() 作
作![]() 于點
于點![]() ,
,
由![]() ,
,
得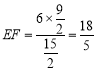 ,即點
,即點![]() 的縱坐標為
的縱坐標為![]() ,
,
又點![]() 在直線
在直線![]() :
:![]() 上,
上,
∴![]() , 解得
, 解得 ![]() , ∴
, ∴![]()
由于EP∥DB,所以可設直線![]() :
:![]() ,
,
∵![]() 在直線
在直線![]() 上
上
∴![]() , 解得
, 解得 ![]() ,
,
∴直線![]() :
:![]() ,
,
令![]() ,則
,則![]() ,
,
解得![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖![]() ,一枚質地均勻的正四面體骰子,它有四個面并分別標有數字
,一枚質地均勻的正四面體骰子,它有四個面并分別標有數字![]() ,
,![]() ,
,![]() ,
,![]() ,如圖
,如圖![]() ,正方形
,正方形![]() 頂點處各有一個圈.跳圈游戲的規則為:游戲者每擲一次骰子,骰子著地一面上的數字是幾,就沿正方形的邊順時針方向連續跳幾個邊長.如:若從圖
頂點處各有一個圈.跳圈游戲的規則為:游戲者每擲一次骰子,骰子著地一面上的數字是幾,就沿正方形的邊順時針方向連續跳幾個邊長.如:若從圖![]() 起跳,第一次擲得
起跳,第一次擲得![]() ,就順時針連續跳
,就順時針連續跳![]() 個邊長,落到圈
個邊長,落到圈![]() ;若第二次擲得
;若第二次擲得![]() ,就從
,就從![]() 開始順時針連續跳
開始順時針連續跳![]() 個邊長,落到圈
個邊長,落到圈![]() ;
;![]() 設游戲者從圈
設游戲者從圈![]() 起跳.
起跳.
(![]() )嘉嘉隨機擲一次骰子,求落回到圈
)嘉嘉隨機擲一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇隨機擲兩次骰子,用列表法求最后落回到圈
)淇淇隨機擲兩次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她與嘉嘉落回到圈
,并指出她與嘉嘉落回到圈![]() 的可能性一樣嗎?
的可能性一樣嗎?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC三個頂點的坐標分別是A(2,2)、B(2,0),C(4,2).
(1)在平面直角坐標系中畫出△ABC;
(2)若將(1)中的△ABC平移,使點B的對應點B′坐標為(6,2),畫出平移后的△A′B′C′;
(3)求△A′B′C′的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,AOBC的頂點A、C的坐標分別為A(﹣2,0)、C(0,3),反比例函數的圖象經過點B.
(1)求反比例函數的表達式;
(2)這個反比例函數的圖象與一個一次函數的圖象交于點B、D(m,1),根據圖象回答:當x取何值時,反比例函數的值大于一次函數的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校與圖書館在同一條筆直道路上,甲從學校去圖書館,乙從圖書館回學校,甲,乙兩人都勻速步行且同時出發,乙先到達目的地,兩人之間的距離![]() (米)與時間
(米)與時間![]() (分鐘)之間的函數關系如圖所示,根據圖象信息回答下列問題:
(分鐘)之間的函數關系如圖所示,根據圖象信息回答下列問題:

(1)圖書館與學校之間的距離為 米;
(2)當![]() 分鐘時,甲乙兩人相遇;
分鐘時,甲乙兩人相遇;
(3)乙的速度為 米/分鐘;
(4)![]() 點的坐標為 .
點的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)探究發現
數學活動課上,小明說“若直線![]() 向左平移3個單位,你能求平移后所得直線所對應函數表達式嗎?”
向左平移3個單位,你能求平移后所得直線所對應函數表達式嗎?”
經過一番討論,小組成員展示了他們的解答過程:
在直線![]() 上任取點
上任取點![]() ,
,
向左平移3個單位得到點![]()
設向左平移3個單位后所得直線所對應的函數表達式為![]() .
.
因為![]() 過點
過點![]() ,
,
所以![]() ,
,
所以![]() ,
,
填空:所以平移后所得直線所對應函數表達式為
(2)類比運用
已知直線![]() ,求它關于
,求它關于![]() 軸對稱的直線所對應的函數表達式;
軸對稱的直線所對應的函數表達式;
(3)拓展運用
將直線![]() 繞原點順時針旋轉90°,請直接寫出:旋轉后所得直線所對應的函數表達式 .
繞原點順時針旋轉90°,請直接寫出:旋轉后所得直線所對應的函數表達式 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 為邊
為邊![]() 上一點,
上一點,![]() 為邊
為邊![]() 的中點,過點
的中點,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,連結
,連結![]() .
.
(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若點![]() 為邊
為邊![]() 的中點,當線段BC與線段AC滿足什么數量關系時,四邊形
的中點,當線段BC與線段AC滿足什么數量關系時,四邊形![]() 為正方形.
為正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】珠海市水務局對某小區居民生活用水情況進行了調査.隨機抽取部分家庭進行統計,繪制成如下尚未完成的頻數分布表和頻率分布直方圖.請根據圖表,解答下列問題:
月均用水量(單位:噸 | 頻數 | 頻率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合計 | d | 1.00 |

(1)b= ,c= ,并補全頻數分布直方圖;
(2)為鼓勵節約用水用水,現要確定一個用水量標準P(單位:噸),超過這個標準的部分按1.5倍的價格收費,若要使60%的家庭水費支出不受影響,則這個用水量標準P= 噸;
(3)根據該樣本,請估計該小區400戶家庭中月均用水量不少于5噸的家庭約有多少戶?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com