【題目】已知△ABC是等邊三角形，點D、E分別在AC、BC上，且CD=BE，
（1）求證：△ABE≌△BCD；
（2）求出∠AFB的度數．
【答案】（1）見解析；（2）120°．
【解析】
試題分析：（1）根據等邊三角形的性質得出AB=BC，∠BAC=∠C=∠ABE=60°，根據SAS推出△ABE≌△BCD；
（2）根據△ABE≌△BCD，推出∠BAE=∠CBD，根據三角形的外角性質求出∠AFB即可．
解：（1）∵△ABC是等邊三角形，
∴AB=BC（等邊三角形三邊都相等），
∠C=∠ABE=60°，（等邊三角形每個內角是60°）．
在△ABE和△BCD中，
，
∴△ABE≌△BCD（SAS）．
（2）∵△ABE≌△BCD（已證），
∴∠BAE=∠CBD（全等三角形的對應角相等），
∵∠AFD=∠ABF+∠BAE（三角形的一個外角等于與它不相鄰的兩個內角之和）
∴∠AFD=∠ABF+∠CBD=∠ABC=60°，
∴∠AFB=180°﹣60°=120°．
能考試期末沖刺卷系列答案科目：初中數學 來源： 題型：
【題目】已知△ABC中，∠ABC=∠ACB，D為線段CB上一點（不與C、B重合），點E為射線CA上一點，∠ADE=∠AED．設∠BAD=α，∠CDE=β．
（1）如圖（1），
①若∠BAC=42°，∠DAE=30°，則α= ，β= ．
②若∠BAC=54°，∠DAE=36°，則α= ，β= ．
③寫出α與β的數量關系，并說明理由；
（2）如圖（2），當E點在CA的延長線上時，其它條件不變，請直接寫出α與β的數量關系．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等腰三角形ABC的底邊BC長為4，面積是16，腰AC的垂直平分線EF分別交AC，AB邊于E，F點
若點D為BC邊的中點，點M為線段EF上一動點，則
周長的最小值為
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O為平面直角坐標系的原點，點A在x軸上，△OAB是邊長為2的等邊三角形，以點O為旋轉中心，將△OAB按順時針方向旋轉60°，得到△OA′B′，畫出△OA′B′，寫出點A′，B′的坐標．
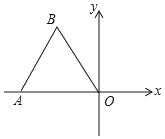
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，半徑為1個單位的圓片上有一點A與數軸上的原點重合，AB是圓片的直徑．(注：結果保留π )
(1)把圓片沿數軸向右滾動半周，點B到達數軸上點C的位置，點C表示的數是 數(填“無理”或“有理”)，這個數是 ；
(2)把圓片沿數軸滾動2周，點A到達數軸上點D的位置，點D表示的數是 ；
(3)圓片在數軸上向右滾動的周數記為正數，圓片在數軸上向左滾動的周數記為負數，依次運動情況記錄如下：+2，﹣1，+3，﹣4，﹣3．
①第 次滾動后，A點距離原點最近，第 次滾動后，A點距離原點最遠．
②當圓片結束運動時，A點運動的路程共有 ，此時點A所表示的數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了了解某校學生對以下四個電視節目：
最強大腦
、
中國詩詞大會、
朗讀者、
出彩中國人的喜愛情況，隨機抽取了部分學生進行調查，要求每名學生選出并且只能選出一個自己最喜愛的節目，根據調查結果，繪制了如下兩幅不完整的統計圖．
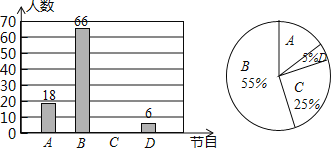
請你根據圖中所提供的信息，完成下列問題：
本次調查的學生人數為______；
在扇形統計圖中，A部分所占圓心角的度數為______；
請將條形統計圖補充完整；
若該校共有3000名學生，估計該校最喜愛
中國詩詞大會的學生有多少名．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，經過坐標原點的拋物線C1：y=ax2+bx與x軸的另一交點為M，它的頂點為點A，將C1繞原點旋轉180°，得到拋物線C2 ， C2與x軸的另一交點為N，頂點為點B，連接AM，MB，BN，NA，當四邊形AMBN恰好是矩形時，則b的值（ ）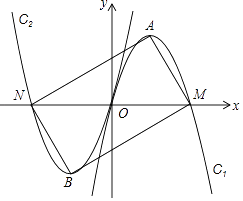
A.2 
B.﹣2
C.2 
D.﹣2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
