
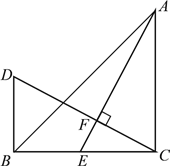
【題目】如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上,BE的延長線交AC于點F,且BF⊥AC,垂足為F,∠BAC=45°
求證:△AEF≌△BCF.

科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AC=BC,AE是BC邊上的中線,過點C作CF⊥AE,垂足為F,過B作BD⊥BC交CF的延長線于D;若AC=12cm,求BD的長;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)計算:(a-2)(a2+2a+4)= ,
(2x-y)(4x2+2xy+y2)= .
(2)上面的整式乘法計算結果很簡單,由此又發現一個新的乘法公式: _________________________(請用含a、b的字母表示)
(3)下列各式能用你發現的乘法公式計算的是( )
A.(a-3)(a2-3a+9) B.(2m-n)(2m2+2mn+n2)
C.(4-x)(16+4x+x2) D.(m-n)(m2+2mn+n2)
(4)直接用公式計算: ![]() =
=
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線AB與x軸,y軸交于點A(10,0),B(0,-10),直線MT垂直于直線AB,垂足為M,與y軸交于點T(0,-2) .
(1)求點M的坐標;
(2)在線段MT的延長線上找一點N,使MT=TN,求點N的坐標;
(3)若點D在x軸上,∠ABD=60°,E點在線段BD上運動,∠AEB的平分線交AB于點P,∠EAB的平分線交線段BD于點Q,AQ與EP交于點R. ![]() 的值是多少?
的值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,有一個等腰直角三角形AOB,∠OAB=90°,直角邊AO在x軸上,且AO=1.將Rt△AOB繞原點O順時針旋轉90°得到等腰直角三角形A1OB1,且A1O=2AO,再將Rt△A1OB1繞原點O順時針旋轉90°得到等腰三角形A2OB2,且A2O=2A1O……依此規律,得到等腰直角三角形A2 017OB2 017.則點B2 017的坐標( )

A. (22 017,-22 017) B. (22 016,-22 016) C. (22 017,22 017) D. (22 016,22 016)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將一塊等腰直角三角板ABC放在第一象限,斜靠在兩條坐標軸上,∠ACB=900,且A(0,4),點C(2,0),BE⊥x軸于點E,一次函數y=x+b經過點B,交y軸于點D。
(1)求證;△AOC≌△CEB
(2)求△ABD的面積。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com