
【題目】如果有一列數,從這列數的第2個數開始,每一個數與它的前一個數的比等于同一個非零的常數,這樣的一列數就叫做等比數列(Geometric Sequences).這個常數叫做等比數列的公比,通常用字母q表示(q≠0).
(1)觀察一個等比列數1,![]() ,…,它的公比q= ;如果an(n為正整數)表示這個等比數列的第n項,那么a18= ,an= ;
,…,它的公比q= ;如果an(n為正整數)表示這個等比數列的第n項,那么a18= ,an= ;
(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步驟進行:
令S=1+2+4+8+16+…+230…①
等式兩邊同時乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以 ![]()
請根據以上的解答過程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若數列a1,a2,a3,…,an,從第二項開始每一項與前一項之比的常數為q,請用含a1,q,n的代數式表示an;如果這個常數q≠1,請用含a1,q,n的代數式表示a1+a2+a3+…+an.
科目:初中數學 來源: 題型:
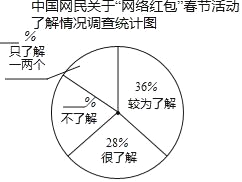
【題目】“網絡紅包”是互聯網運營商、商家通過組織互聯網線上活動、派發紅包的互聯網工具,是朋友間互道祝福的表達形式之一.“網絡紅包”春節活動已經逐漸深入到大眾的生活中,得到了人們較為廣泛的關注.根據某咨詢公司(2018年中國春節“網絡紅包”專題調查報告》顯示:在接受調查的8萬名網民中,對“網絡紅包”春節話動了解程度的占比方面,“較為了解”和“很了解”的網民共占比64%,分別占比36%和28%.在“不了解”和“只了解一兩個“的受訪網民中,“不了解”的網民人數比“只了解一兩個”的網民人數多25%.如圖是該咨詢公司繪制的“中國網民關于‘網絡紅包’春節活動了解情況調查”統計圖(不完整).
請根據以上信息解答下列問題:
(1)在受訪的網民中,“不了解”和“只了解一兩個”的網民人數共有 萬人,其中“不了解”的網民人數是 萬人;
(2)請將扇形統計圖補充完整;
(3)2017除夕晚上小聰和爸爸、媽媽一起玩微信搶紅包游戲,他們約定由爸爸在家人微信群中先后發兩次“拼手氣紅包”,每次發放的紅包數是3個,每個紅包抽到的金額隨機(每兩個紅包的金額都不相等),每次誰抽到紅包的金額最大誰就是“手氣最佳”者,求兩次游戲中小聰都能獲得“手氣最佳”的概率為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC,BD相交于點O,∠ADB=30°,E為BC邊上一點,∠AEB=45°,CF⊥BD于F.下列結論:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正確的結論有( )
AO,④CE=CF.正確的結論有( )
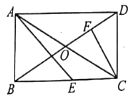
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點C是直線AB上一點,AC=6cm,BC=4cm,點M、N分別是AC、BC的中點;
(1)如圖,點C在線段AB上,求線段MN的長;
(2)若點C在線段AB的延長線上,其他條件不變,則線段MN的長為_______cm.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的中線BD,CE交于點O,F,G分別是BO,CO的中點.
(1)填空:四邊形DEFG是 四邊形.
(2)若四邊形DEFG是矩形,求證:AB=AC.
(3)若四邊形DEFG是邊長為2的正方形,試求△ABC的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學活動課上,同學們利用如圖所示的程序進行計算,計算按箭頭指向循環進行.
如,當初始輸入5時,即![]() =5,第1次計算結果為16,第2次計算結果為8,第3次計算結果為4,…
=5,第1次計算結果為16,第2次計算結果為8,第3次計算結果為4,…

(1)當初始輸入1時,第1次計算結果為 ;
(2)當初始輸入4時,第3次計算結果為 ;
(3)當初始輸入3時,依次計算得到的所有結果中,有 個不同的值,第20次計算結果為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
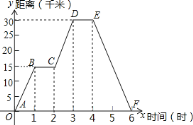
【題目】小明同學騎自行車去濱海港郊游,中途休息了一段時間。如圖表示他離家的距離y(千米)與所用的時間s(小時)之間關系的函數圖像
(1)根據圖像回答:小明家離濱海港 千米,小明到達濱海港時用了 小時;
(2)直線CD的函數解析式為 ;
(3)小明出發幾小時,離家12千米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com