
【題目】閱讀下面文字,然后回答問題.
大家知道![]() 是無理數,而無理數是無限不循環小數,所以
是無理數,而無理數是無限不循環小數,所以![]() 的小數部分我們不可能全部寫出來,由于
的小數部分我們不可能全部寫出來,由于![]() 的整數部分是1,將
的整數部分是1,將![]() 減去它的整數部分,差就是它的小數部分,因此
減去它的整數部分,差就是它的小數部分,因此![]() 的小數部分可用
的小數部分可用![]() ﹣1表示.
﹣1表示.
由此我們得到一個真命題:如果![]() =x+y,其中x是整數,且0<y<1,那么x=1,y=
=x+y,其中x是整數,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
請解答下列問題:
(1)如果![]() =a+b,其中a是整數,且0<b<1,那么a= ,b= ;
=a+b,其中a是整數,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整數,且0<d<1,那么c= ,d= ;
=c+d,其中c是整數,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°.
(1)尺規作圖:作AB邊上的垂直平分線DE,交AC于點D,交AB于點E.(保留作圖痕跡,不要求寫作法和證明);
(2)在(1)的條件下,連接BD,當BC=5cm,AB=13cm時,求△BCD的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角板是學習數學的重要工具,將一副三角板中的兩塊直角三角板的直角頂點![]() 按如圖方式疊放在一起,當
按如圖方式疊放在一起,當![]() 且點
且點![]() 在直線
在直線![]() 的上方時,解決下列問題:(友情提示:
的上方時,解決下列問題:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,則
,則![]() 的度數為 ;
的度數為 ;
②若![]() ,則
,則![]() 的度數為 ;
的度數為 ;
(2)由(1)猜想![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
(3)這兩塊三角板是否存在一組邊互相平行?若存在,請直接寫出![]() 的角度所有可能的值(不必說明理由);若不存在,請說明理由.
的角度所有可能的值(不必說明理由);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)在圖1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,則能得如下兩個結論:① DC = BC; ②AD+AB=AC.請你證明結論②;
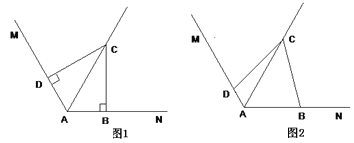
(2)在圖2中,把(1)中的條件“∠ABC=∠ADC=90°”改為∠ABC+∠ADC=180°,其他條件不變,則(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠要新建一個800平方米的長方形場地,且其長、寬的比為5:2.
(1)求這個長方形場地的長和寬為多少米?
(2)某個正方形場地的周圍有一圈金屬柵欄圍墻,如果把原來面積為900平方米的正方形場地的柵欄圍墻全部利用,來作為新場地的長方形圍墻,柵欄圍墻是否夠用?為什么?(提示:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB于點R,PS⊥AC于點S,若PR=PS,則下列結論正確的個數是( )
(1)PQ=PB; (2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPC
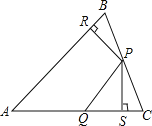
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生會向全校1900名學生發起了愛心捐款活動,為了解捐款情況,學生會隨機調查了部分學生的捐款金額,并用得到的數據繪制了如下統計圖1和圖2,請根據相關信息,解答系列問題: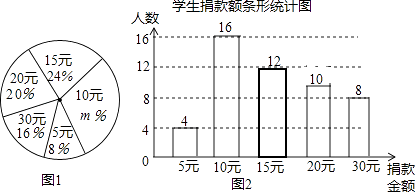
(1)本次接受隨機抽樣調查的學生人數為人,圖1中m的值是 .
(2)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(3)根據樣本數據,估計該校本次活動捐款金額為10元的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com