
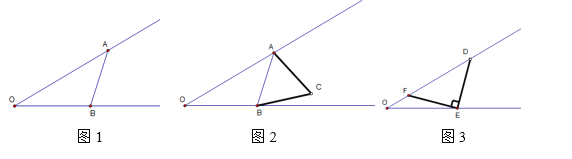
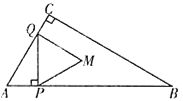
【題目】當一個角固定不變,而某種圖形在該角的內部變化,則我們稱這個角為墻角.
(1)如圖1,墻角![]() =30°,如果AB=3,長度不變,在角內滑動,當OA=6時,則求出此時OB的長度.
=30°,如果AB=3,長度不變,在角內滑動,當OA=6時,則求出此時OB的長度.
(2)如圖2,墻角![]() =30°,如果在AB的右邊作等邊
=30°,如果在AB的右邊作等邊![]() ,AB=3,長度不變,滑動過程中,請求出點O與點C的最大距離.
,AB=3,長度不變,滑動過程中,請求出點O與點C的最大距離.
(3)如圖3,墻角![]() =
=![]() 時,如果點E是
時,如果點E是![]() 一條邊上的一個點,
一條邊上的一個點,![]() =90°,其兩條邊與
=90°,其兩條邊與![]() 另一條邊交于點F與點D,求
另一條邊交于點F與點D,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)過A點作OB的垂線AE,證明E點與B點重合即可求得OB的長;
(2)在點A運動過程中,AB長不變,∠AOB=30°不變,考慮到同弧所對的圓周角不變,所以構造半徑為3且過AB兩點的圓O',易知O O'=3,C O'=![]() ,當O、O'、C三點共線時,得最值;
,當O、O'、C三點共線時,得最值;
(3)過點F做FG![]() OE與點G,過點D做DH
OE與點G,過點D做DH![]() OE與點H,根據
OE與點H,根據![]() =
=![]() ,不妨設FG=3a,DH=3b,則OG=4a,OH=4b,GH=4b-4a (
,不妨設FG=3a,DH=3b,則OG=4a,OH=4b,GH=4b-4a (![]() ),證明
),證明![]() ∽
∽![]() ,根據相似三角形的對應邊成比例求解即可.
,根據相似三角形的對應邊成比例求解即可.
(1)如圖1,過A點作AE⊥OB,
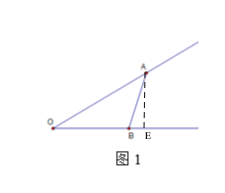
∵∠O=30°,OA=6
∴AE=![]()
又AB=3,AE⊥OB
∴B點與E點重合
∴![]()
(2)如圖2,在C點的另一側作等邊三角形ABO',連接O O',連接O'C交AB于點,則∠A O'B=60°,以O'為圓心,以3為半徑作圓,則A、B點在圓上,又因為∠AOB=30°=![]() ∠A O'B,故O點在圓上,當O、O'、C三點共線時,點O與點C的距離最大.
∠A O'B,故O點在圓上,當O、O'、C三點共線時,點O與點C的距離最大.
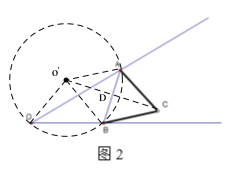
∵△ABC、△AB O'為等邊三角形
∴四邊形AO'BC為菱形
∴O'C 與AB互相垂直平分,AD=![]() ,∠CAD=60°
,∠CAD=60°
∴CD=![]()
∴O'C=2CD=![]()
∴當O、O'、C三點共線時,點O與點C的最大距離為當OO'+O'C![]()
(3)如圖:過點F做FG![]() OE與點G,過點D做DH
OE與點G,過點D做DH![]() OE與點H,
OE與點H,
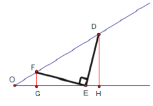
∴∠DHE=∠FGE=90°
∵![]() =
=![]() ,設FG=3a,DH=3b,則OG=4a,OH=4b,GH=4b-4a (
,設FG=3a,DH=3b,則OG=4a,OH=4b,GH=4b-4a (![]() )
)
∵![]() =90°
=90°
∴∠DEH+∠FEG=90°,∠FEG+∠EFG=90°
∴∠DEH=∠EFG=
∴![]() ∽
∽![]()
∴![]()
∴![]()
即![]()
∴![]()
∵![]()
∴![]()
化簡后得到:![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∵FG//DH,
∴![]() =
=![]() =
=![]()
![]()
![]() =
=![]()


科目:初中數學 來源: 題型:
【題目】賀歲片《流浪地球》被稱為開啟了中國科幻片的大門,2019也被稱為中國科幻片的元年.某電影院為了全面了解觀眾對《流浪地球》的滿意度情況,進行隨機抽樣調查,分為四個類別:A.非常滿意;B.滿意;C.基本滿意;D.不滿意.依據調查數據繪制成圖1和圖2的統計圖(不完整).根據以上信息,解答下列問題:

(1)本次接受調查的觀眾共有 人;
(2)扇形統計圖中,扇形C的圓心角度數是 .
(3)請補全條形統計圖;
(4)春節期間,該電影院來觀看《流浪地球》的觀眾約3000人,請估計觀眾中對該電影滿意(A、B、C類視為滿意)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數的圖象與x軸相交于A(3,0)、B(1,0)兩點,與y軸相交于點C(0,3),點C.D是二次函數圖象上的一對對稱點,一次函數的圖象過點B,D.
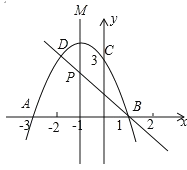
(1)D點坐標;
(2)求二次函數的解析式;
(3)根據圖象直接寫出使一次函數值小于二次函數值的x的取值范圍;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市為慶祝開業舉辦大酬賓抽獎活動,凡在開業當天進店購物的顧客,都能獲得一次抽獎的機會,抽獎規則如下:在一個不透明的盒子里裝有分別標有數字1、2、3的3個小球,它們的形狀、大小、質地完全相同,顧客先從盒子里隨機取出一個小球,記下小球上標有的數字,然后把小球放回盒子并攪拌均勻,再從盒子中隨機取出一個小球,記下小球上標有的數字,并計算兩次記下的數字之和,若兩次所得的數字之和為6,則可獲得50元代金券一張;若所得的數字之和為5,則可獲得30元代金券一張;若所得的數字之和為4,則可獲得15元代金券一張;其它情況都不中獎.
(1)請用列表或樹狀圖的方法(選其中一種即可),把抽獎一次可能出現的結果表示出來.
(2)假如你參加了該超市開業當天的一次抽獎活動,求能中獎的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校開設“慈善基金”活動以來,受到同學們的廣泛幫助,學校為了解全校學生捐款的情況,隨機調查了部分學生的捐款金額,并制成如圖不完整的統計圖表.
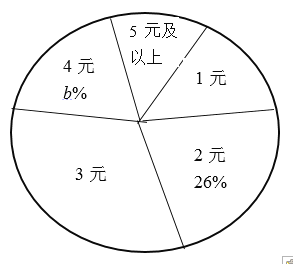
捐款金額 | 1元 | 2元 | 3元 | 4元 | 5元及以上 |
人數 | 7 | 13 | a | 10 | 3 |
請你根據統計圖表中的信息,解答下列問題:
(1)a= ,b= ;
(2)該調查統計數據的中位數是 ,眾數是 ;
(3)請計算扇形統計圖中的3元所對應的圓心角的度數;
(4)若該校共有2000名學生,根據調查結果,統計該校學生在5元及以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
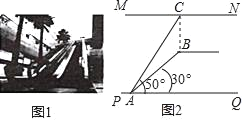
【題目】如圖1是某商場從一樓到二樓的自動扶梯,圖2是側面示意圖,MN是二樓樓頂,MN∥PQ,點C在MN上,且位于自動扶梯頂端B點的正上方,BC⊥MN.測得AB=10米,在自動扶梯底端A處測得點C的仰角為50°,點B的仰角為30°,求二樓的層高BC(結果保留根號)
(參考數據:sin50°=0.77,cos50°=0.64,tan50°=1.20)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年“五一”節,小明外出爬山,他從山腳爬到山頂的過程中,中途休息了一段時間.設他從山腳出發后所用時間為t(分鐘),所走路程為s(米),s與t之間的函數關系如圖所示,則下列說法中,錯誤的是( )
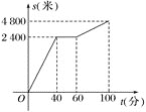
A. 小明中途休息用了20分鐘 B. 小明休息前爬山的速度為每分鐘60米
C. 小明在上述過程中所走路程為7 200米 D. 小明休息前后爬山的平均速度相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 從點
從點![]() 出發以每秒2個單位的速度沿
出發以每秒2個單位的速度沿![]() 向終點
向終點![]() 運動,過點
運動,過點![]() 作
作![]() 的垂線交折線
的垂線交折線![]() 于點
于點![]() ,當點
,當點![]() 不和
不和![]() 的頂點重合時,以
的頂點重合時,以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,使點
,使點![]() 和點
和點![]() 在直線
在直線![]() 的同側,設點
的同側,設點![]() 的運動時間為
的運動時間為![]() (秒).
(秒).
(1)求等邊三角形![]() 的邊長(用含
的邊長(用含![]() 的代數式表示);
的代數式表示);
(2)當點![]() 落在
落在![]() 的邊
的邊![]() 上時,求
上時,求![]() 的值;
的值;
(3)設![]() 與
與![]() 重合部分圖形的面積為
重合部分圖形的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式;
的函數關系式;
(4)作直線![]() ,設點
,設點![]() 關于直線
關于直線![]() 的對稱點分別為
的對稱點分別為![]() ,直接寫出
,直接寫出![]() 時
時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,對“隔離直線”給出如下定義:點
中,對“隔離直線”給出如下定義:點![]() 是圖形
是圖形![]() 上的任意一點,點
上的任意一點,點![]() 是圖形
是圖形![]() 上的任意一點,若存在直線
上的任意一點,若存在直線![]() :
:![]() 滿足
滿足![]() 且
且![]() ,則稱直線
,則稱直線![]() :
:![]() 是圖形
是圖形![]() 與
與![]() 的“隔離直線”,如圖
的“隔離直線”,如圖![]() ,直線
,直線![]() :
:![]() 是函數
是函數![]() 的圖像與正方形
的圖像與正方形![]() 的一條“隔離直線”.
的一條“隔離直線”.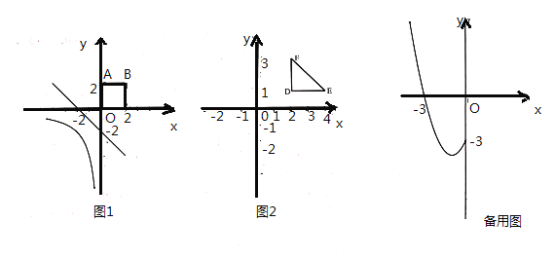
(1)在直線①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是圖
中,是圖![]() 函數
函數![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”的為 .
的“隔離直線”的為 .
(2)如圖![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的兩腰分別與坐標軸平行,直角頂點
的兩腰分別與坐標軸平行,直角頂點![]() 的坐標是
的坐標是![]() ,⊙O的半徑為
,⊙O的半徑為![]() ,是否存在
,是否存在![]() 與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
(3)正方形![]() 的一邊在
的一邊在![]() 軸上,其它三邊都在
軸上,其它三邊都在![]() 軸的左側,點
軸的左側,點![]() 是此正方形的中心,若存在直線
是此正方形的中心,若存在直線![]() 是函數
是函數![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”,請直接寫出
的“隔離直線”,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com