
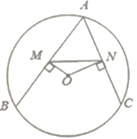
【題目】如圖,點A、B、C在半徑為2的圓O上,且∠BAC=60°,作OM⊥AB于點M,ON⊥AC于點N,連接MN,則MN的長為( )
A. 1B. ![]() C. 2D. 2
C. 2D. 2![]()
【答案】B
【解析】
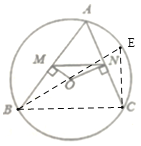
連接OB并延長交圓O于E,則BE為圓O直徑,連接BC、CE,由圓周角定理可得∠BEC=60°,由BE是直徑可知∠BCE=90°,利用∠BEC的余弦值可得BC的長,根據垂徑定理可得AM=BM,AN=CN,即可證明MN是△ABC的中位線,根據三角形中位線定理即可求出MN的長.
連接OB并延長交圓O于E,則BE為圓O直徑,連接BC、CE,
∵∠BAC和∠AEC都是![]() 所對圓周角,
所對圓周角,
∴∠BAC=∠BEC=60°,
∵BE是直徑,
∴∠BCE=90°,BE=4,
∴BC=BE![]() sin60°=4×
sin60°=4×![]() =2
=2![]() ,
,
∵OM⊥AB,ON⊥AC,
∴AM=BM,AN=CN,
∴MN是△ABC的中位線,
∴MN=![]() BC=
BC=![]() .
.
故選B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,正方形ABCD中,AB=4cm,點P從點D出發沿DA向點A勻速運動,速度是1cm/s,同時,點Q從點A出發沿AB方向,向點B勻速運動,速度是2cm/s,連接PQ、CP、CQ,設運動時間為t(s)(0<t<2)
(1)是否存在某一時刻t,使得PQ∥BD?若存在,求出t值;若不存在,說明理由
(2)設△PQC的面積為s(cm2),求s與t之間的函數關系式;
(3)如圖2,連接AC,與線段PQ相交于點M,是否存在某一時刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
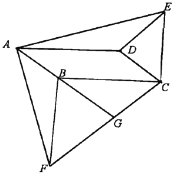
【題目】如圖,在口ABCD中,分別以邊BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,連接AF,AE.
(1)求證:△ABF≌△EDA;
(2)延長AB與CF相交于G,若AF⊥AE,求證BF⊥BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)在一個不透明的紙箱里裝有紅、黃、藍三種顏色的小球,它們除顏色外完全相同,其中紅球有2個,黃球有1個,藍球有1個.現有一張電影票,小明和小亮決定通過摸球游戲定輸贏(贏的一方得電影票).游戲規則是:兩人各摸1次球,先由小明從紙箱里隨機摸出1個球,記錄顏色后放回,將小球搖勻,再由小亮隨機摸出1個球并記錄顏色.若兩人摸到的球顏色相同,則小明贏,否則小亮贏.這個游戲規則對雙方公平嗎?請你利用樹狀圖或列表法說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
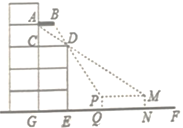
【題目】周末,小凱和同學帶著皮尺,去測量楊大爺家露臺遮陽蓬的寬度,如圖,由于無法直接測量,小凱便在樓前面的地面上選擇了一條直線EF,通過在直線EF上選點觀測,發現當他位于N點時,他的視線從M點通過露臺D點正好落在遮陽蓬A點處:當他位于Q點時,視線從P點通過露臺D點正好落在遮陽蓬B點處,這樣觀測到兩個點A,B間的距離即為遮陽蓬的寬.已知AB∥CD∥EF,點C在AG上,AG、DE、PQ、MN均為垂直于EF,MN=PQ,露臺的寬CD=GE,測得GE=5米,EN=13.2米,QN=6.2,請你根據以上信息,求出遮陽蓬的寬AB是多少米?(結果精確到0.01米)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的大致圖象如圖所示,頂點坐標為(﹣2,﹣9a),下列結論:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有兩個根x1和x2,且x1<x2,則﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四個根,則這四個根的和為﹣4.其中正確的結論有( )
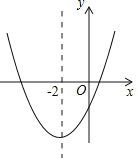
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠MON=30°,B為OM上一點,BA⊥ON于點A,四邊形ABCD為正方形,P為射線BM上一動點,連結CP,將CP繞點C順時針方向旋轉90°得CE,連接BE,若AB=2,則BE的最小值為( )
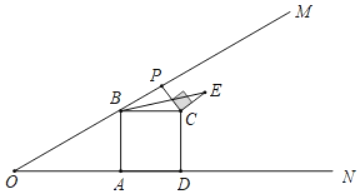
A. ![]() +1B. 2
+1B. 2![]() ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題發現:
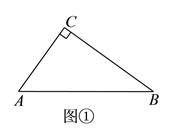
(![]() )如圖①,
)如圖①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上任意一點,則
邊上任意一點,則![]() 的最小值為__________.
的最小值為__________.
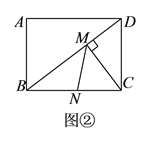
(![]() )如圖②,矩形
)如圖②,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、點
、點![]() 分別在
分別在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
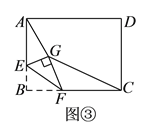
(![]() )如圖③,矩形
)如圖③,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上一點,且
邊上一點,且![]() ,點
,點![]() 是
是![]() 邊上的任意一點,把
邊上的任意一點,把![]() 沿
沿![]() 翻折,點
翻折,點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() 、
、![]() ,四邊形
,四邊形![]() 的面積是否存在最小值,若存在,求這個最小值及此時
的面積是否存在最小值,若存在,求這個最小值及此時![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com