
【題目】如圖,AB是⊙O的弦,D為OA半徑的中點(diǎn),過D作CD⊥OA交弦AB于點(diǎn)E,交⊙O于點(diǎn)F,且CE=CB.
(1)求證:BC是⊙O的切線;
(2)連接AF、BF,求∠ABF的度數(shù);
(3)如果BE=10,sinA=![]() ,求⊙O的半徑.
,求⊙O的半徑.

【答案】(1)詳見解析;(2)30°;(3)![]() .
.
【解析】試題分析:(1)連接![]() 圓的半徑相等和已知條件證明
圓的半徑相等和已知條件證明![]() ,即可證明
,即可證明![]() 是
是![]() 的切線;
的切線;
(2)連接![]() 首先證明
首先證明![]() 是等邊三角形,再利用圓周角定理:同弧所對(duì)的圓周角是所對(duì)圓心角的一半即可求出∠
是等邊三角形,再利用圓周角定理:同弧所對(duì)的圓周角是所對(duì)圓心角的一半即可求出∠![]() 的度數(shù);
的度數(shù);
(3)過點(diǎn)O作OG⊥AB于點(diǎn)G,得到AG=BG,在![]() 中
中![]() 設(shè)DE=5x,則AE=13x,AD=12x,AO=24x,把
設(shè)DE=5x,則AE=13x,AD=12x,AO=24x,把![]() 表示出來,在
表示出來,在![]() 中,用三角函數(shù)的知識(shí)列出方程,解出
中,用三角函數(shù)的知識(shí)列出方程,解出![]() 得值,即可求出半徑.
得值,即可求出半徑.
試題解析:(1)證明:連接OB,
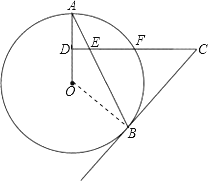
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC.
又∵CD⊥OA.
![]()
![]()
∴OB⊥BC
∴BC是![]() 的切線.
的切線.
(2)連接OF,AF,BF,
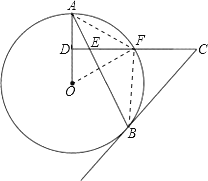
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等邊三角形,
![]()
![]()
(3)連接OF,AF,
∵DA=
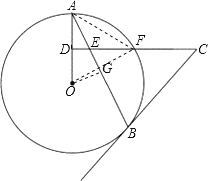
∴AF=OF=OA,
過點(diǎn)O作OG⊥AB于點(diǎn)G,得到AG=BG,
在![]() 中
中![]()
設(shè)DE=5x,則AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
則![]()
又∵![]() 中,
中, ![]() 則
則![]()
則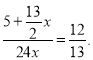
解得![]()
![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】把一張矩形紙片ABCD按如圖方式折疊,使點(diǎn)A與點(diǎn)E重合,點(diǎn)C與點(diǎn)F重合(E,F兩點(diǎn)均在BD上),折痕分別為BH,DG.
(1)求證:BH∥DG;
(2)求證:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求線段CG的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
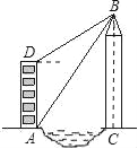
【題目】如圖,小莉的家在錦江河畔的電梯公寓AD內(nèi),她家的河對(duì)岸新建了一座大廈BC,為了測量大廈的高度,小莉在她家的樓底A處測得大廈頂部B的仰角為60°,爬上樓頂D處測得大廈頂部B的仰角為30°,已知電梯公寓高82米,請(qǐng)你幫助小莉計(jì)算出大廈的高度BC及大廈與電梯公寓間的距離AC.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,
,![]() 、
、![]() 為直線
為直線![]() 上兩點(diǎn),且滿足
上兩點(diǎn),且滿足![]() ,連接
,連接![]() 、
、![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .
.
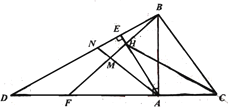
(1)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)若點(diǎn)![]() 是線段
是線段![]() 上的動(dòng)點(diǎn),連
上的動(dòng)點(diǎn),連![]() 并延長交
并延長交![]() 于
于![]() ,當(dāng)
,當(dāng)![]() 在線段
在線段![]() 的什么位置上時(shí),
的什么位置上時(shí),![]() ?請(qǐng)說明理由;
?請(qǐng)說明理由;
(3)在(2)的結(jié)論下,判斷線段![]() 、
、![]() 、
、![]() 的數(shù)量關(guān)系.請(qǐng)說明理由.
的數(shù)量關(guān)系.請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AD,AF分別為△ABC的中線和高,BE為△ABD的角平分線.
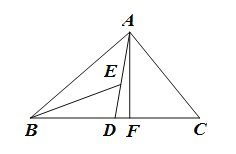
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面積為40,BD=5,求AF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)y=kx+b的圖象經(jīng)過A、B兩點(diǎn),與x軸交于點(diǎn)C,則此一次函數(shù)的解析式為__________,△AOC的面積為_________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖1,在△ABC中,∠A![]() ,P是BC邊上的一點(diǎn),
,P是BC邊上的一點(diǎn),![]() ,
,![]() 是點(diǎn)P關(guān)于AB、AC的對(duì)稱點(diǎn),連結(jié)
是點(diǎn)P關(guān)于AB、AC的對(duì)稱點(diǎn),連結(jié)![]() ,分別交AB、AC于點(diǎn)D、E.
,分別交AB、AC于點(diǎn)D、E.
①若![]() ,求
,求![]() 的度數(shù);
的度數(shù);
②請(qǐng)直接寫出∠A與![]() 的數(shù)量關(guān)系:___________________________;
的數(shù)量關(guān)系:___________________________;
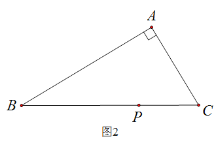
(2)如圖2,在△ABC中,若∠BAC![]() ,用三角板作出點(diǎn)P關(guān)于AB、AC的對(duì)稱點(diǎn)
,用三角板作出點(diǎn)P關(guān)于AB、AC的對(duì)稱點(diǎn)![]() 、
、![]() ,(不寫作法,保留作圖痕跡),試判斷點(diǎn)
,(不寫作法,保留作圖痕跡),試判斷點(diǎn)![]() ,
,![]() 與點(diǎn)A是否在同一直線上,并說明理由.
與點(diǎn)A是否在同一直線上,并說明理由.
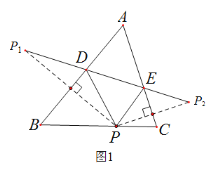
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)求一次函數(shù)y=2x-2的圖象l1與y=![]() x-1的圖象l2的交點(diǎn)P的坐標(biāo).
x-1的圖象l2的交點(diǎn)P的坐標(biāo).
(2)求直線![]() 與
與![]() 軸交點(diǎn)A的坐標(biāo); 求直線
軸交點(diǎn)A的坐標(biāo); 求直線![]() 與x軸的交點(diǎn)B的坐標(biāo);
與x軸的交點(diǎn)B的坐標(biāo);
(3)求由三點(diǎn)P、A、B圍成的三角形的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是作一個(gè)角的角平分線的方法:以![]() 的頂點(diǎn)
的頂點(diǎn)![]() 為圓心,以任意長為半徑畫弧,分別交
為圓心,以任意長為半徑畫弧,分別交![]() 于
于![]() 兩點(diǎn),再分別以
兩點(diǎn),再分別以![]() 為圓心,大于
為圓心,大于![]() 長為半徑作畫弧,兩條弧交于點(diǎn)
長為半徑作畫弧,兩條弧交于點(diǎn)![]() ,作射線
,作射線![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .
.

(1)若![]() ,求
,求![]() 的度數(shù);
的度數(shù);
(2)若![]() ,垂足為
,垂足為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com