
【題目】如圖,拋物線G:y1=a(x+1)2+2與H:y2=﹣(x﹣2)2﹣1交于點B(1,﹣2),且分別與y軸交于點D、E.過點B作x軸的平行線,交拋物線于點A、C,則以下結論:①無論x取何值,y2總是負數;②拋物線H可由拋物線G向右平移3個單位,再向下平移3個單位得到;③當﹣3<x<1時,隨著x的增大,y1﹣y2的值先增大后減小;④四邊形AECD為正方形.其中正確的是( )

A.①③④B.①②④C.②③④D.①②③④
【答案】B
【解析】
①由非負數的性質,即可證得y2=﹣(x﹣2)2﹣1≤﹣1<0,即可得無論x取何值,y2總是負數;
②由拋物線l1:y1=a(x+1)2+2與l2:y2=﹣(x﹣2)2﹣1交于點B(1,﹣2),可求得a的值,然后由拋物線的平移的性質,即可得l2可由l1向右平移3個單位,再向下平移3個單位得到;
③由 y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,可得隨著x的增大,y1﹣y2的值減小;
④首先求得點A,C,D,E的坐標,即可證得AF=CF=DF=EF,又由AC⊥DE,即可證得四邊形AECD為正方形.
解:①∵(x﹣2)2≥0,
∴﹣(x﹣2)2≤0,
∴y2=﹣(x﹣2)2﹣1≤﹣1<0,
∴無論x取何值,y2總是負數;
故①正確;
②∵拋物線G:y1=a(x+1)2+2與拋物線H:y2=﹣(x﹣2)2﹣1交于點B(1,﹣2),
∴當x=1時,y=﹣2,
即﹣2=a(1+1)2+2,
解得:a=﹣1;
∴y1=﹣(x+1)2+2,
∴H可由G向右平移3個單位,再向下平移3個單位得到;
故②正確;
③∵y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,
∴隨著x的增大,y1﹣y2的值減小;
故③錯誤;
④設AC與DE交于點F,
∵當y=﹣2時,﹣(x+1)2+2=﹣2,
解得:x=﹣3或x=1,
∴點A(﹣3,﹣2),
當y=﹣2時,﹣(x﹣2)2﹣1=﹣2,
解得:x=3或x=1,
∴點C(3,﹣2),
∴AF=CF=3,AC=6,
當x=0時,y1=1,y2=﹣5,
∴DE=6,DF=EF=3,
∴四邊形AECD為平行四邊形,
∴AC=DE,
∴四邊形AECD為矩形,
∵AC⊥DE,
∴四邊形AECD為正方形.
故④正確.
故選:B.



科目:初中數學 來源: 題型:
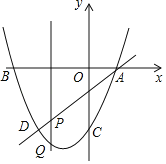
【題目】如圖,拋物線y=ax2+bx﹣3過A(1,0),B(﹣3,0),直線AD交拋物線于點D,點D的橫坐標為﹣2,點P(m,n)是線段AD上的動點.
(1)求直線AD及拋物線的解析式;
(2)過點P的直線垂直于x軸,交拋物線于點Q,求線段PQ的長度l與m的關系式,m為何值時,PQ最長?
(3)在平面內是否存在整點(橫、縱坐標都為整數)R,使得P,Q,D,R為頂點的四邊形是平行四邊形?若存在,直接寫出點R的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
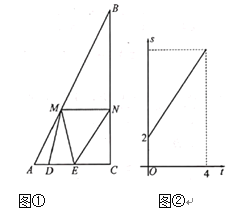
【題目】如圖①,![]() 中,
中,![]() ,點
,點![]() 從點
從點![]() 出發沿
出發沿![]() 方向勻速運動,速度為1
方向勻速運動,速度為1![]() 點
點![]() 是
是![]() 上位于點
上位于點![]() 右側的動點,點
右側的動點,點![]() 是
是![]() 上的動點,在運動過程中始終保持
上的動點,在運動過程中始終保持![]() ,
,![]() cm.過
cm.過![]() 作
作![]() 交
交![]() 于
于![]() ,當點
,當點![]() 與點
與點![]() 重合時點
重合時點![]() 停止運動.設
停止運動.設![]() 的而積為
的而積為![]() ,點
,點![]() 的運動時問為
的運動時問為![]() ,
,![]() 與
與![]() 的函數關系如圖②所示:
的函數關系如圖②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)設四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
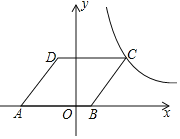
【題目】如圖,在平面直角坐標系中,點O為坐標原點,菱形ABCD的頂點B在x軸的正半軸上,點A坐標為(-4,0),點D的坐標為(-1,4),反比例函數![]() 的圖象恰好經過點C,則k的值為______.
的圖象恰好經過點C,則k的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在矩形![]() 中,
中,![]() 為
為![]() 的中點,一塊足夠大的三角板的直角頂點與點
的中點,一塊足夠大的三角板的直角頂點與點![]() 重合,將三角板繞點
重合,將三角板繞點![]() 旋轉,三角板的兩直角邊分別交
旋轉,三角板的兩直角邊分別交![]() 或它們的延長線)于點
或它們的延長線)于點![]() ,設
,設![]() ,下列四個結論:①
,下列四個結論:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正確的個數是( )
,正確的個數是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
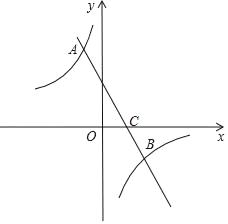
【題目】如圖,直線y=kx+b(k≠0)與雙曲線y=![]() (m≠0)交于點A(﹣
(m≠0)交于點A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直線與雙曲線的解析式.
(2)點P在x軸上,如果S△ABP=3,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
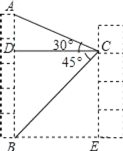
【題目】小宇在學習解直角三角形的知識后,萌生了測量他家對面位于同一水平面的樓房高度的想法,他站在自家C處測得對面樓房底端B的俯角為45°,測得對面樓房頂端A的仰角為30°,并量得兩棟樓房間的距離為9米,請你用小宇測得的數據求出對面樓房AB的高度.(結果保留到整數,參考數據:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
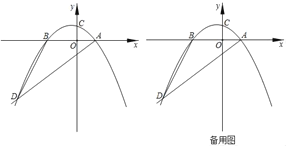
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c(a≠0)交x軸于點A(2,0),B(﹣3,0),交y軸于點C,且經過點d(﹣6,﹣6),連接AD,BD.
(1)求該拋物線的函數關系式;
(2)若點M為X軸上方的拋物線上一點,能否在點A左側的x軸上找到另一點N,使得△AMN與△ABD相似?若相似,請求出此時點M、點N的坐標;若不存在,請說明理由;
(3)若點P是直線AD上方的拋物線上一動點(不與A,D重合),過點P作PQ∥y軸交直線AD于點Q,以PQ為直徑作⊙E,則⊙E在直線AD上所截得的線段長度的最大值等于 .(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了扎實推進精準扶貧工作,某市出臺了民生兜底、醫保脫貧、教育教助、產業扶持、養老托管和易地搬遷這六種幫扶措施,每戶貧困戶都享受了2到5種幫扶措施,現把享受了2種、3種、4種和5種幫扶措施的貧困戶分別稱為![]() 類貧困戶。為檢查幫扶措施是否落實,隨機抽取了若干貧困戶進行調查,現將收集的數據繪制成下面兩幅不完整的統計圖:
類貧困戶。為檢查幫扶措施是否落實,隨機抽取了若干貧困戶進行調查,現將收集的數據繪制成下面兩幅不完整的統計圖:
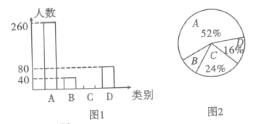
請根據圖中信息回答下面的問題:
(1)本次抽樣調查了多少戶貧困戶;
(2)抽查了多少戶![]() 類貧困戶?并補全統計圖;
類貧困戶?并補全統計圖;
(3)若該地共有1300戶貧困戶,請估計至少得到4項幫扶措施的大約有多少戶;
(4)為更好地做好精準扶貧工作,現準備從![]() 類貧困戶中的甲、乙、丙、丁四戶中隨機選取兩戶進行重點幫扶,請用樹狀圖或列表法求出恰好選中甲和丁的概率.
類貧困戶中的甲、乙、丙、丁四戶中隨機選取兩戶進行重點幫扶,請用樹狀圖或列表法求出恰好選中甲和丁的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com