
【題目】如圖①,![]() 中,
中,![]() ,點
,點![]() 從點
從點![]() 出發沿
出發沿![]() 方向勻速運動,速度為1
方向勻速運動,速度為1![]() 點
點![]() 是
是![]() 上位于點
上位于點![]() 右側的動點,點
右側的動點,點![]() 是
是![]() 上的動點,在運動過程中始終保持
上的動點,在運動過程中始終保持![]() ,
,![]() cm.過
cm.過![]() 作
作![]() 交
交![]() 于
于![]() ,當點
,當點![]() 與點
與點![]() 重合時點
重合時點![]() 停止運動.設
停止運動.設![]() 的而積為
的而積為![]() ,點
,點![]() 的運動時問為
的運動時問為![]() ,
,![]() 與
與![]() 的函數關系如圖②所示:
的函數關系如圖②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)設四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
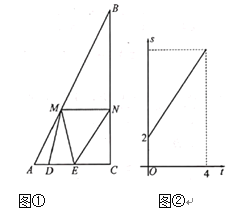
【答案】(1)6,12;(2)![]() 時,
時,![]() 有最大值16.(3)
有最大值16.(3)![]() 或
或![]()
【解析】
(1)當t=4時,點E與C重合,此時AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
由圖分析當t=0時,S![]() =2.設M到AC的距離為h,所以
=2.設M到AC的距離為h,所以![]() DE
DE![]() h=2,所以h=2.易求得tan∠A=2,再在Rt
h=2,所以h=2.易求得tan∠A=2,再在Rt![]() 中,解直角三角形可以求出AC的長.
中,解直角三角形可以求出AC的長.
(2) 四邊形![]() 的面積等于三角形MDE和三角形MNE的和,用含有t的式子表示出四邊形MDEN的面積,再求最值;
的面積等于三角形MDE和三角形MNE的和,用含有t的式子表示出四邊形MDEN的面積,再求最值;
(3)兩個三角形中已有![]() ,如若再找到一對角相等,兩三角形相似,故需分情況進行討論:當
,如若再找到一對角相等,兩三角形相似,故需分情況進行討論:當![]() 或
或![]() 時,兩三角形相似.
時,兩三角形相似.
解:(1)由圖可知:當t=4時,點E與C重合,此時AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
當t=0時,S![]() =2.設M到AC的距離為h,所以
=2.設M到AC的距離為h,所以![]() DE
DE![]() h=2,所以h=2.
h=2,所以h=2.
∴tan∠A=![]() =2.
=2.
在Rt![]() 中,tan∠A=
中,tan∠A=![]() =2.
=2.
∴BC=2AC=12.
(2)作![]() 于點
于點![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]()
![]() ,
,
根據題意,![]() ,
,
∴![]() 時,
時,![]() 有最大值16.
有最大值16.
(3)假設存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.
∵![]() ,∴
,∴![]() .
.
①當![]() 時,
時,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
②當![]() 時,
時,![]() ,此時
,此時![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() (舍去)
(舍去)
∴![]() 或
或![]() 時,以
時,以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.



科目:初中數學 來源: 題型:
【題目】現在正是草莓熱銷的季節,某水果零售商店分兩批次從批發市場共購進草莓40箱,已知第一、二次進貨價分別為每箱50元、40元,且第二次比第一次多付款700元.
(1)設第一、二次購進草莓的箱數分別為a箱、b箱,求a,b的值;
(2)若商店對這40箱草莓先按每箱60元銷售了x箱,其余的按每箱35元全部售完.
①求商店銷售完全部草莓所獲利潤y(元)與x(箱)之間的函數關系式;
②當x的值至少為多少時,商店才不會虧本.(注:按整箱出售,利潤=銷售總收入-進貨總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,平行四邊形OABC的頂點A在x軸上,OC=4,∠AOC=60°,且以點O為圓心,任意長為半徑畫弧,分別交OA、OC于點D、E;再分別以點D、點E為圓心,大于![]() DE的長度為半徑畫弧,兩弧相交于點F,過點O作射線OF,交BC于點P.則點P的坐標為( )
DE的長度為半徑畫弧,兩弧相交于點F,過點O作射線OF,交BC于點P.則點P的坐標為( )
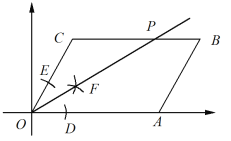
A.(4,2![]() )B.(6,2
)B.(6,2![]() )C.(2
)C.(2![]() ,4)D.(2
,4)D.(2![]() ,6)
,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“新冠肺炎防控”知識宣傳活動中,某社區對居民掌握新冠肺炎防控知識的情況進行調查.其中![]() 、
、![]() 兩區分別有500名居民,社區從中各隨機抽取50名居民進行相關知識測試,并將成績進行整理得到部分信息:
兩區分別有500名居民,社區從中各隨機抽取50名居民進行相關知識測試,并將成績進行整理得到部分信息:
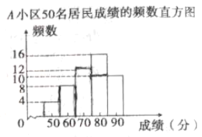
(信息一)![]() 小區50名居民成績的頻數直方圖如圖(每一組含前一個邊界值,不含后一個邊界值);
小區50名居民成績的頻數直方圖如圖(每一組含前一個邊界值,不含后一個邊界值);
(信息二)圖中,![]() 小區從左往右第四組的成績如下
小區從左往右第四組的成績如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 、
、![]() 兩小區各50名居民成績的平均數、中位數、眾數、優秀率(80分及以上為優秀)、方差等數據如下(部分空缺):
兩小區各50名居民成績的平均數、中位數、眾數、優秀率(80分及以上為優秀)、方差等數據如下(部分空缺):
小區 | 平均數 | 中位數 | 眾數 | 優秀率 | 方差 |
| 75.1 | 79 |
| 277 | |
| 75.1 | 77 | 76 |
| 211 |
根據以上信息,回答下列問題:
(1)求![]() 小區50名居民成績的中位數;
小區50名居民成績的中位數;
(2)請估計![]() 小區500名居民中能超過平均數的有多少人?
小區500名居民中能超過平均數的有多少人?
(3)請盡量從多個角度比較、分析![]() ,
,![]() 兩小區居民掌握新冠防控知識的情況.
兩小區居民掌握新冠防控知識的情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
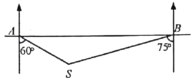
【題目】一艘輪船在![]() 處測得燈塔
處測得燈塔![]() 在船的南偏東60°方向,輪船繼續向正東航行30海里后到達
在船的南偏東60°方向,輪船繼續向正東航行30海里后到達![]() 處,這時測得燈塔
處,這時測得燈塔![]() 在船的南偏西75°方向,則燈塔
在船的南偏西75°方向,則燈塔![]() 離觀測點
離觀測點![]() 、
、![]() 的距離分別是( )
的距離分別是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣為落實“精準扶貧惠民政策”,計劃將某村的居民自來水管道進行改造.該工程若由甲隊單獨施工恰好在規定時間內完成;若乙隊單獨施工,則完成工程所需天數是規定天數的1.5倍.如果由甲、乙隊先合作施工15天,那么余下的工程由甲隊單獨完成還需5天.
(1)這項工程的規定時間是多少天?
(2)為了縮短工期以減少對居民用水的影響,工程指揮部最終決定該工程由甲、乙兩隊合作完成.則甲、乙兩隊合作完成該工程需要多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀對學生的成長有著深遠的影響.某中學為了解學生每周課余閱讀的時間,在本校隨機抽取若干名學生進行調查,并依據調查結果經制了以下不完整的統計圖表.
組別 | 時間(小時) | 頻數(人數) | 頻率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合計 | 1 |
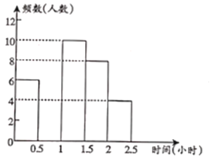
請根據圖表中的信息,解答下列問題:
(1)表中的![]() ,
,![]() ,將頻數分布直方圖補全;
,將頻數分布直方圖補全;
(2)估計該校2000名學生中,每周課余閱讀時間不足1小時的學生大約有多少名?
(3)![]() 組的4人中,有1名男生和3名女生,該校計劃在
組的4人中,有1名男生和3名女生,該校計劃在![]() 組學生中隨機選出兩人向全校同學作讀書心得報告,求抽取的兩名學生剛好是1名男生和1名女生的概率.
組學生中隨機選出兩人向全校同學作讀書心得報告,求抽取的兩名學生剛好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線G:y1=a(x+1)2+2與H:y2=﹣(x﹣2)2﹣1交于點B(1,﹣2),且分別與y軸交于點D、E.過點B作x軸的平行線,交拋物線于點A、C,則以下結論:①無論x取何值,y2總是負數;②拋物線H可由拋物線G向右平移3個單位,再向下平移3個單位得到;③當﹣3<x<1時,隨著x的增大,y1﹣y2的值先增大后減小;④四邊形AECD為正方形.其中正確的是( )

A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△OAB中,∠AOB=90°,AO=2,BO=4.將△OAB繞頂點O按順時針方向旋轉到△OA1B1處,此時線段OB1與AB的交點D恰好為線段AB的中點,線段A1B1與OA交于點E,則圖中陰影部分的面積__.
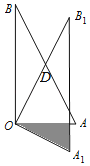
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com