
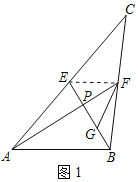
【題目】我們知道三角形任意兩條中線的交點是三角形的重心.重心有如下性質:重心到頂點的距離是重心到對邊中點距離的2倍.請利用該性質解決問題

(1)如圖1,在△ABC中,AF、BE是中線,AF⊥BE于P.若BP=2,∠FAB=30°,則EP= ,FP= ;
(2)如圖1,在△ABC中,BC=a,AC=b,AB=c,AF、BE是中線,AF⊥BE于P.猜想a2、b2、c2三者之間的關系并證明;
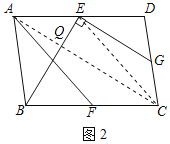
(3)如圖2,在ABCD中,點E、F、G分別是AD、BC、CD的中點,BE⊥BG,AB=3,AD=2![]() ,求AF的長.
,求AF的長.
【答案】(1)1,![]() ;(2)a2+b2=5c2,理由見解析;(3)AF=4
;(2)a2+b2=5c2,理由見解析;(3)AF=4
【解析】
(1)由三角形的重心定理得出BP=2EP=2,AP=2FP,得出EP=1,由直角三角形的性質得出AP=![]() BP=2
BP=2![]() ,即可得出FP=
,即可得出FP=![]() AP=
AP=![]() ;
;
(2)設PF=m,PE=n,由 ![]() ,得到AP=2m,PB=2n,再由勾股定理即可得出結論;
,得到AP=2m,PB=2n,再由勾股定理即可得出結論;
(3)連接AC、EC,由平行四邊形的性質得出AD=BC,AD∥BC,證明四邊形AFCE是平行四邊形,得出AF=CE,由平行線得出△AEQ∽△CBQ,得出![]() ,設AQ=a,EQ=b,則CQ=2a,BQ=2b,證明EG是△ACD的中位線,由三角形中位線定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=
,設AQ=a,EQ=b,則CQ=2a,BQ=2b,證明EG是△ACD的中位線,由三角形中位線定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=![]() ,得出BQ2=4b2=
,得出BQ2=4b2=![]() ,b2=
,b2=![]() ,在Rt△EQC中,由勾股定理求出CE,即可得出AF的長.
,在Rt△EQC中,由勾股定理求出CE,即可得出AF的長.
解:(1)∵在△ABC中,AF、BE是中線,
∴BP=2EP=2,AP=2FP,
∴EP=1,
∵AF⊥BE,∠FAB=30°,
∴AB=2BP=4,
∴AP=![]() ,
,
∴FP=![]() AP=
AP=![]() ;
;
故答案為:1,![]() ;
;
(2)a2+b2=5c2;理由如下:
連接EF,如圖1所示:
∵AF,BE是△ABC的中線,
∴EF是△ABC的中位線,
∴EF∥AB,且EF=![]() AB=
AB=![]() c,
c,
∴![]() ,
,
設PF=m,PE=n,
∴AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2,即4m2+4n2=c2,
在Rt△APE中,(2m)2+n2=(![]() b)2,即4m2+n2=
b)2,即4m2+n2=![]() b2,
b2,
在Rt△FPB中,m2+(2n)2=(![]() a)2,即m2+4n2=
a)2,即m2+4n2=![]() a2,
a2,
∴5m2+5n2=![]() (a2+b2)=
(a2+b2)=![]() c2,
c2,
∴a2+b2=5c2;
(3)連接AC、EC,如圖2所示:
∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC,
∵點E,F分別是AD,BC,CD的中點,
∴AE=CE,
∴四邊形AFCE是平行四邊形,
∴AF=CE,
∵AD∥BC,
∴△AEQ∽△CBQ,
∴![]() ,
,
設AQ=a,EQ=b,則CQ=2a,BQ=2b,
∵點E,G分別是AD,CD的中點,
∴EG是△ACD的中位線,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
由勾股定理得:AB2﹣AQ2=BC2﹣CQ2,
即9﹣a2=(2![]() )2﹣4a2,
)2﹣4a2,
∴3a2=11,
∴a2=![]() ,
,
∴BQ2=4b2=(2![]() )2﹣4×
)2﹣4×![]() =
=![]() ,
,
∴b2=![]() ×
×![]() =
=![]() ,
,
在Rt△EQC中,CE2=EQ2+CQ2=b2+4a2=16,
∴CE=4,
∴AF=4.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一動點從原點O出發,按向上、向右、向下、向右的方向依次不斷地移動,每次移動一個單位,得到點A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么點A2019的坐標為( )
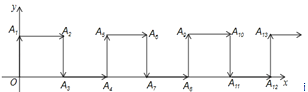
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市經濟技術開發區某智能手機有限公司接到生產300萬部智能手機的訂單,為了盡快交貨,增開了一條生產線,實際每月生產能力比原計劃提高了50%,結果比原計劃提前5個月完成交貨,求每月實際生產智能手機多少萬部.
查看答案和解析>>
科目:初中數學 來源: 題型:
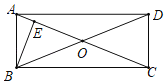
【題目】如圖,ABCD的對角線AC、BD相交于點O,且∠OBC=∠OCB.
(1)求證:四邊形ABCD為矩形;
(2)過B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知鈍角△ABC,老師按照如下步驟尺規作圖: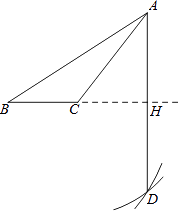
步驟1:以C為圓心,CA為半徑畫弧①;
步驟2:以B為圓心,BA為半徑畫弧②,交弧①于點D;
步驟3:連接AD,交BC延長線于點H.
小明說:圖中的BH⊥AD且平分AD.
小麗說:圖中AC平分∠BAD.
小強說:圖中點C為BH的中點.
他們的說法中正確的是 . 他的依據是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:用3輛A型車和2輛B型車載滿貨物一次可運貨共19噸;用2輛A型車和3輛B型車載滿貨物一次可運貨共21噸.
(1)1輛A型車和1輛B型車都載滿貨物一次分別可以運貨多少噸?
(2)某物流公司現有49噸貨物,計劃同時租用A型車![]() 輛,B型車
輛,B型車![]() 輛,一次運完,且恰好每輛車都載滿貨物.
輛,一次運完,且恰好每輛車都載滿貨物.
①求![]() 、
、![]() 的值;
的值;
②若A型車每輛需租金130元/次,B型車每輛需租金200元/次.請求出租車費用最少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意有理數x,用[x]表示不大于x的最大整數.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下結論正確的是_____.(把你認為正確結論的序號都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[![]() ]=﹣4,則x的取值范圍是﹣
]=﹣4,則x的取值范圍是﹣![]() ≤x<﹣
≤x<﹣![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com