

 時,S與t之間的函數關系式.
時,S與t之間的函數關系式. ;(2)①
;(2)① -2;②
-2;②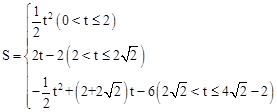 .
. ;(2)①由矩形的性質和已知AD∥BO,可得四邊形ABOD是平行四邊形,從而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,從而由平移的性質可求得t=IM=OM-OI=
;(2)①由矩形的性質和已知AD∥BO,可得四邊形ABOD是平行四邊形,從而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,從而由平移的性質可求得t=IM=OM-OI= -2;②首先確定當0<t≤
-2;②首先確定當0<t≤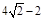 時,矩形EFGH沿y軸向上平移過程中關鍵點的位置,分0<t≤2,2<t≤
時,矩形EFGH沿y軸向上平移過程中關鍵點的位置,分0<t≤2,2<t≤ ,
, <t≤
<t≤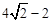 三種情況求出S與t之間的函數關系式.
三種情況求出S與t之間的函數關系式. .
. -2.
-2.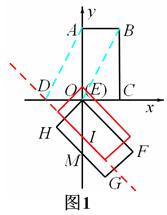
 ,F(
,F( ,-
,- ).
).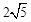 ,
,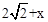 .
. ,解得x=
,解得x=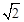 . ∴G(
. ∴G(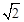 ,-
,-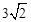 ).
).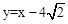 .
.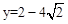 .
.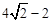 時,就是GF平移到過點C時的位置(如圖5).
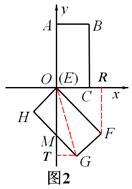
時,就是GF平移到過點C時的位置(如圖5).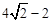 時,幾個關鍵點如圖3,4,5所示:
時,幾個關鍵點如圖3,4,5所示: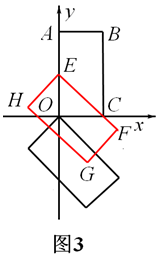
 ,此時,矩形EFGH沿y軸向上平移過程中邊HG經過點O;
,此時,矩形EFGH沿y軸向上平移過程中邊HG經過點O;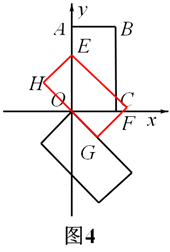
 ,此時,矩形EFGH沿y軸向上平移過程中邊FG經過點C.
,此時,矩形EFGH沿y軸向上平移過程中邊FG經過點C.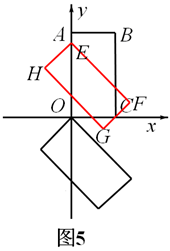
 .
.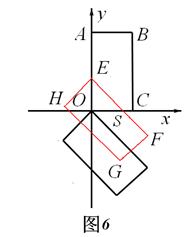
 時,矩形EFHG與矩形OABC重疊部分的面積為直角梯形OEPC的面積(如圖7).此時OE= t,,OC=2.
時,矩形EFHG與矩形OABC重疊部分的面積為直角梯形OEPC的面積(如圖7).此時OE= t,,OC=2.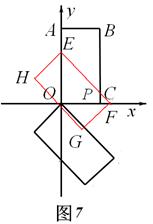
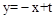 .
.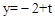 . ∴CP=
. ∴CP=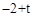 . ∴
. ∴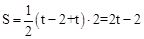 .
. <t≤
<t≤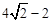 時,矩形EFHG與矩形OABC重疊部分的面積為五邊形EQCUV的面積(如圖8),
時,矩形EFHG與矩形OABC重疊部分的面積為五邊形EQCUV的面積(如圖8),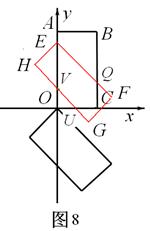
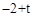 ,OU="OV=" t-
,OU="OV=" t- .
.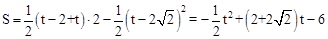 .
.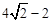 時,S與t之間的函數關系式為
時,S與t之間的函數關系式為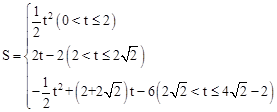 .
.

科目:初中數學 來源:不詳 題型:解答題
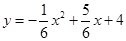 與直線
與直線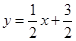 交于點A 、B,與y軸交于點C.
交于點A 、B,與y軸交于點C.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
|
若二次函數y=ax2+bx+c的x與y的部分對應值如下表:則下列說法錯誤的是( )
|
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
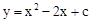 與y軸的交點為(0,﹣3),則下列說法不正確的是【 】
與y軸的交點為(0,﹣3),則下列說法不正確的是【 】| A.拋物線開口向上 |
| B.拋物線的對稱軸是x=1 |
| C.當x=1時,y的最大值為﹣4 |
| D.拋物線與x軸的交點為(-1,0),(3,0) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com