Question

【題目】數和形是數學的兩個主要研究對象，我們經常運用數形結合、數形轉化的方法解決一些數學問題．下面我們來探究“由數思形，以形助數”的方法在解決代數問題中的應用．

探究一：求不等式|x﹣1|＜2的解集

（1）探究|x﹣1|的幾何意義

如圖①，在以O為原點的數軸上，設點A′對應的數是x﹣1，有絕對值的定義可知，點A′與點O的距離為

|x﹣1|，可記為A′O=|x﹣1|．將線段A′O向右平移1個單位得到線段AB，此時點A對應的數是x，點B對應的數是1．因為AB=A′O，所以AB=|x﹣1|，因此，|x﹣1|的幾何意義可以理解為數軸上x所對應的點A與1所對應的點B之間的距離AB．

（2）求方程|x﹣1|=2的解

因為數軸上3和﹣1所對應的點與1所對應的點之間的距離都為2，所以方程的解為3，﹣1．

（3）求不等式|x﹣1|＜2的解集

因為|x﹣1|表示數軸上x所對應的點與1所對應的點之間的距離，所以求不等式解集就轉化為求這個距離小于2的點對應的數x的范圍．請寫出這個解集：_________________________________．

探究二：探究的幾何意義

（1）探究的幾何意義

如圖③，在直角坐標系中，設點M的坐標為（x，y），過M作MP⊥x軸于P，作MQ⊥y軸于Q，則P點坐標為（x，0），Q點坐標為（0，y），OP=|x|，OQ=|y|，在Rt△OPM中，PM=OQ=|y|，則，因此，的幾何意義可以理解為點M（x，y）與點O（0，0）之間的距離MO．

（2）探究的幾何意義

如圖④，在直角坐標系中，設點A′的坐標為（x﹣1，y﹣5），由探究二（1）可知，，將線段A′O先向右平移1個單位，再向上平移5個單位，得到線段AB，此時點A的坐標為（x，y），點B的坐標為（1，5），因為AB=A′O，所以，因此的幾何意義可以理解為點A（x，y）與點B（1，5）之間的距離AB．

（3）探究的幾何意義，根據探究二（2）所得的結論，請寫出的幾何意義可以理解為：________________．

（4）的幾何意義可以理解為：________________________________．

Answer 1

【答案】探究一（3）；探究二（3）點A（x，y）與點B（-3，4）之間的距離AB；（4）點A（x，y）與點B（a，b）之間的距離．

【解析】

探究一（3）由于|x﹣1|表示數軸上x所對應的點與1所對應的點之間的距離，所以求不等式解集就轉化為求這個距離小于2的點對應的數x的范圍，從而畫出數軸即可；

探究二（3）由于的幾何意義可以理解為點A（x，y）與點B（1，5）之間的距離AB，所以可以得到的幾何意義是：點A（x，y）與點B（-3，4）之間的距離AB；

（4）由前面的探究可知的幾何意義可以理解為：點A（x，y）與點B（a，b）之間的距離．

解：探究一：（3）如圖所示，

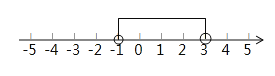
的解集是；

探究二：（3）如圖，

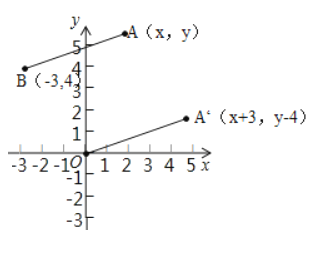
在直角坐標系中，設點A′的坐標為（x+3，y﹣4），

由探究二（1）可知，，

將線段A′O先向左平移3個單位，再向上平移4個單位，得到線段AB，

此時點A的坐標為（x，y），點B的坐標為（-3，4），

∵AB=A′O，

∴，．

∴的幾何意義是：點A（x，y）與點B（-3，4）之間的距離AB；

（4）根據前面的探究可知的幾何意義可以理解為：點A（x，y）與點B（a，b）之間的距離．