
【題目】閱讀下列材料,并完成相應(yīng)任務(wù):
黃金分割
天文學(xué)家開普勒把黃金分割稱為神圣分割,并指出畢達(dá)哥拉斯定理(勾股定理)和黃金分割是幾何中的雙寶,前者好比黃金,后者堪稱珠寶,歷史上最早正式在書中使用“黃金分割”這個(gè)名稱的是歐姆,19世紀(jì)以后“黃金分割”的說法逐漸流行起來,黃金分割被廣泛應(yīng)用于建筑等領(lǐng)域.黃金分割指把一條線段分為兩部分,使其中較長部分與線段總長之比等于較短部分與較長部分之比,該比值為![]() .用下面的方法(如圖①)就可以作出已知線段
.用下面的方法(如圖①)就可以作出已知線段![]() 的黃金分割點(diǎn)
的黃金分割點(diǎn)![]() :
:

①以線段![]() 為邊作正方形
為邊作正方形![]() ,
,
②取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,
③延長![]() 到
到![]() ,使
,使![]() ,
,
④以線段![]() 為邊作正方形
為邊作正方形![]() ,點(diǎn)
,點(diǎn)![]() 就是線段
就是線段![]() 的黃金分割點(diǎn).
的黃金分割點(diǎn).
以下是證明點(diǎn)![]() 就是線段
就是線段![]() 的黃金分割點(diǎn)的部分過程:
的黃金分割點(diǎn)的部分過程:
證明:設(shè)正方形![]() 的邊長為1,則
的邊長為1,則![]() ,
,
![]() 為
為![]() 中點(diǎn),
中點(diǎn),
![]() ,
,
![]() 在
在![]() 中,
中,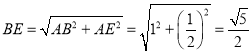 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任務(wù):
(1)補(bǔ)全題中的證明過程;
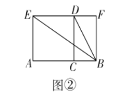
(2)如圖②,點(diǎn)![]() 為線段
為線段![]() 的黃金分割點(diǎn),分別以
的黃金分割點(diǎn),分別以![]() 為邊在線段
為邊在線段![]() 同側(cè)作正方形
同側(cè)作正方形![]() 和矩形
和矩形![]() ,連接
,連接![]() .求證:
.求證:![]() ;
;
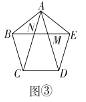
(3)如圖③,在正五邊形![]() 中,對角線
中,對角線![]() 與
與![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() 求證:點(diǎn)
求證:點(diǎn)![]() 是
是![]() 的黃金分割點(diǎn).
的黃金分割點(diǎn).
【答案】(1)詳見解析;(2)詳見解析;(3)詳見解析
【解析】
(1)設(shè)正方形ABCD的邊長為1,則AB=AD=1,由勾股定理得出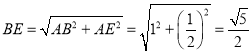 ,得出
,得出![]() ,求出
,求出![]() ,由正方形的性質(zhì)得出
,由正方形的性質(zhì)得出![]() ,求出
,求出![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
(2)由正方形和矩形的性質(zhì)得出∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,由點(diǎn)C為線段AB的黃金分割點(diǎn),得出![]() ,因此
,因此![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
(3)根據(jù)正五邊形的性質(zhì)得到∠DAE=∠DAE,∠ADE=∠AEM=36°,推出△AME∽△AED,根據(jù)相似三角形的性質(zhì)得到∴AE:AD=AM:AE,得到AE2=ADAM,等量代換即可得到結(jié)論.
(1)證明:設(shè)正方形ABCD的邊長為1,則AB=AD=1,
∵E為AD中點(diǎn),
∴AE=![]() ,
,
∴在Rt△BAE中,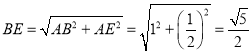
∵EF=BE
∴![]()
∴![]() ,
,
∵四邊形AFGH是正方形,
∴![]() ,
,
∴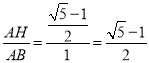 ,
,
∴點(diǎn)H是線段AB的黃金分割點(diǎn);
(2)證明:∵四邊形ACDE是正方形,四邊形CBFD是矩形,
∴∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,
∵點(diǎn)C為線段AB的黃金分割點(diǎn),
∴![]() ,
,
∴![]() ,
,
∴△EAB∽△BCD;
(3)證明:∵五邊形ABCDE是正五邊形,
∴∠BAE=∠AED=![]() (5-2)×180°=108°,AB=AE=DE,
(5-2)×180°=108°,AB=AE=DE,
∴∠ABE=∠AEM=∠DAE=∠ADE=![]() (180°-108°)=36°,
(180°-108°)=36°,
∵∠DAE=∠DAE,∠ADE=∠AEM=36°,
∴△AME∽△AED,
∴AE:AD=AM:AE,
∴AE2=ADAM,
∵AE=DE=DM,/span>
∴DM2=ADAM,
∴點(diǎn)M是AD的黃金分割點(diǎn).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,正方形
中,正方形![]() 的邊長為2,函數(shù)
的邊長為2,函數(shù)![]() 的圖象經(jīng)過點(diǎn)B,與直線
的圖象經(jīng)過點(diǎn)B,與直線![]() 交于點(diǎn)D.
交于點(diǎn)D.
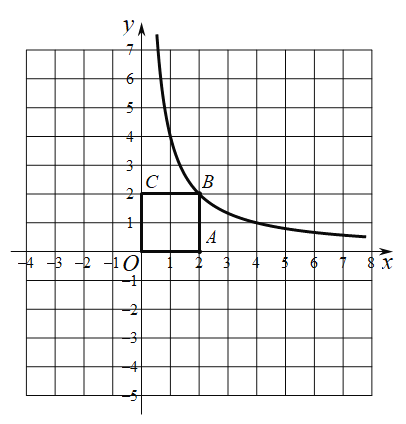
(1)求k的值;
(2)直線![]() 與
與![]() 邊所在直線交于點(diǎn)M,與x軸交于點(diǎn)N.
邊所在直線交于點(diǎn)M,與x軸交于點(diǎn)N.
①當(dāng)點(diǎn)D為![]() 中點(diǎn)時(shí),求b的值;
中點(diǎn)時(shí),求b的值;
②當(dāng)![]() 時(shí),結(jié)合函數(shù)圖象,直接寫出b的取值范圍.
時(shí),結(jié)合函數(shù)圖象,直接寫出b的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為![]() 的正方形ABCD中,點(diǎn)E,F是對角線AC的三等分點(diǎn),點(diǎn)P在正方形的邊上,則滿足PE+PF=
的正方形ABCD中,點(diǎn)E,F是對角線AC的三等分點(diǎn),點(diǎn)P在正方形的邊上,則滿足PE+PF=![]() 的點(diǎn)P的個(gè)數(shù)是( )
的點(diǎn)P的個(gè)數(shù)是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
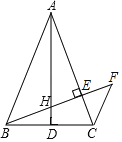
【題目】如圖,在△ABC中,AB=AC,AD是邊BC上的中線,BE⊥AC于點(diǎn)E,交AD于點(diǎn)H過點(diǎn)C作CF∥AB交BE的延長線于點(diǎn)F.
(1)求證:△ABH∽△BFC;
(2)求證:BH2=HEHF;
(3)若AB=2,∠BAC=45°,求BH的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
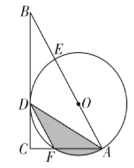
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分線,經(jīng)過
的平分線,經(jīng)過![]() 兩點(diǎn)的圓的圓心
兩點(diǎn)的圓的圓心![]() 恰好落在
恰好落在![]() 上,
上,![]() 分別與
分別與![]() 交于點(diǎn)
交于點(diǎn)![]() .若
.若![]() .則圖中陰影部分的面積為( )
.則圖中陰影部分的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校舉行了自貢市創(chuàng)建全國文明城市知識競賽活動(dòng),初一年級全體同學(xué)參加了知識競賽.
收集教據(jù):現(xiàn)隨機(jī)抽取了初一年級![]() 名同學(xué)的“創(chuàng)文知識競賽”成績,分?jǐn)?shù)如下(單位:分):
名同學(xué)的“創(chuàng)文知識競賽”成績,分?jǐn)?shù)如下(單位:分):
整理分析數(shù)據(jù):
成績 | 頻數(shù)(人數(shù)) |
|
|
|
|
|
|
|
|
(1)請將圖表中空缺的部分補(bǔ)充完整;
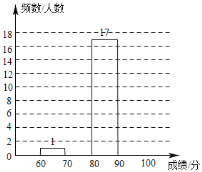
(2)學(xué)校決定表彰“創(chuàng)文知識競賽”成績在![]() 分及其以上的同學(xué).根據(jù)上面統(tǒng)計(jì)結(jié)果估計(jì)該校初一年級
分及其以上的同學(xué).根據(jù)上面統(tǒng)計(jì)結(jié)果估計(jì)該校初一年級![]() 人中,約有多少人將獲得表彰;
人中,約有多少人將獲得表彰;
(3)“創(chuàng)文知識競賽”中,受到表彰的小紅同學(xué)得到了印有龔扇、剪紙、彩燈、恐龍圖案的四枚紀(jì)念章,她從中選取兩枚送給弟弟,則小紅送給弟弟的兩枚紀(jì)念章中,恰好有恐龍圖案的概率是______________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
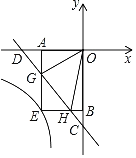
【題目】如圖,在平面直角坐標(biāo)系xOy中,直線y=﹣x﹣2與x軸,y軸分別交于點(diǎn)D,C.點(diǎn)G,H是線段CD上的兩個(gè)動(dòng)點(diǎn),且∠GOH=45°,過點(diǎn)G作GA⊥x軸于A,過點(diǎn)H作HB⊥y軸于B,延長AG,BH交于點(diǎn)E,則過點(diǎn)E的反比例函數(shù)y=![]() 的解析式為_____.
的解析式為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
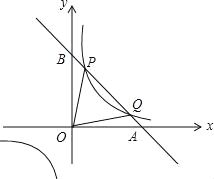
【題目】已知直線y=kx+b與x軸、y軸分別交于A、B兩點(diǎn),與反比例函數(shù)交于一象限內(nèi)的P(![]() ,n),Q(4,m)兩點(diǎn),且tan∠BOP=
,n),Q(4,m)兩點(diǎn),且tan∠BOP=![]() :
:
(1)求反比例函數(shù)和直線的函數(shù)表達(dá)式;
(2)求△OPQ的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
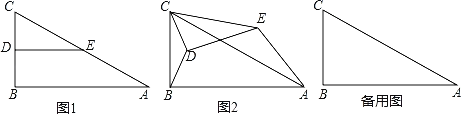
【題目】如圖1,在Rt△ABC中,∠B=90°,AB=4,BC=2,點(diǎn)D、E分別是邊BC、AC的中點(diǎn),連接DE.將△CDE繞點(diǎn)C逆時(shí)針方向旋轉(zhuǎn),記旋轉(zhuǎn)角為α.
(1)問題發(fā)現(xiàn)
①當(dāng)α=0°時(shí),![]() =_______;
=_______;
②當(dāng)α=180°時(shí),![]() =______.
=______.
(2)拓展探究
試判斷:當(dāng)0°≤α<360°時(shí),![]() 的大小有無變化?請僅就圖2的情形給出證明.
的大小有無變化?請僅就圖2的情形給出證明.
(3)問題解決
△CDE繞點(diǎn)C逆時(shí)針旋轉(zhuǎn)至A、B、E三點(diǎn)在同一條直線上時(shí),求線段BD的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com