
【題目】如圖,在平面直角坐標系xOy中,直線y=﹣x﹣2與x軸,y軸分別交于點D,C.點G,H是線段CD上的兩個動點,且∠GOH=45°,過點G作GA⊥x軸于A,過點H作HB⊥y軸于B,延長AG,BH交于點E,則過點E的反比例函數y=![]() 的解析式為_____.
的解析式為_____.
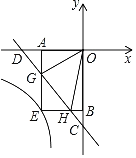
【答案】y=![]()
【解析】
過點G作GP⊥GO,交OH的延長線于點P,過點P作PN⊥AE,交AE延長線于N,設點A(-![]() ,0)則AO=
,0)則AO=![]() ,DO=2,AD=2-
,DO=2,AD=2-![]() ,由“AAS”可證△GAO≌△PNG,可得NP=AG=2-
,由“AAS”可證△GAO≌△PNG,可得NP=AG=2-![]() ,AO=GN=
,AO=GN=![]() ,可求點P坐標,求出一次函數解析式,可求點H的縱坐標,即可求解.
,可求點P坐標,求出一次函數解析式,可求點H的縱坐標,即可求解.
解:如圖,過點G作GP⊥GO,交OH的延長線于點P,過點P作PN⊥AE,交AE延長線于N,
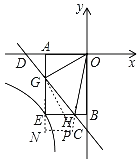
設點A(-![]() ,0)
,0)
∴AO=![]() ,
,
∵直線y=﹣x﹣2與x軸,y軸分別交于點D,C,
∴點D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣![]() ,
,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣![]() ,
,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣![]() ,AO=GN=
,AO=GN=![]() ,
,
∴AN=2,
∴點P(2﹣2![]() ,﹣2),
,﹣2),
∴直線OP解析式為:y=![]() x,
x,
聯立方程組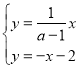
∴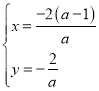
∴點H的縱坐標為![]() ,
,
∴點E(![]() ,
,![]() )
)
∵反比例函數y=![]() 的圖象過點E,
的圖象過點E,
∴k=![]() ×(
×(![]() )=2,
)=2,
∴反比例函數解析式為:y=![]() ,
,
故答案為:y=![]() .
.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:
【題目】如圖1,等邊三角形![]() 中,D為
中,D為![]() 邊上一點,滿足
邊上一點,滿足![]() ,連接
,連接![]() ,以點A為中心,將射線
,以點A為中心,將射線![]() 順時針旋轉60°,與
順時針旋轉60°,與![]() 的外角平分線
的外角平分線![]() 交于點E.
交于點E.
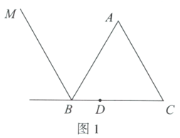
(1)依題意補全圖1;
(2)求證:![]() ;
;
(3)若點B關于直線![]() 的對稱點為F,連接
的對稱點為F,連接![]() .
.
①求證:![]() ;
;
②若![]() 成立,直接寫出
成立,直接寫出![]() 的度數為_________°.
的度數為_________°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,
上,![]() ;
;
①如圖![]() ,若
,若![]() ,且點
,且點![]() 是
是![]() 中點,求證
中點,求證![]() ;
;
②如圖![]() ,若
,若![]() ,且
,且![]() ,求證:
,求證:![]() ;
;
(2)如圖![]() ,當
,當![]() ,
,![]() 時,點
時,點![]() 以
以![]() 的速度從
的速度從![]() 到
到![]() ,點
,點![]() 以
以![]() 的速度從
的速度從![]() 到
到![]() ,當點
,當點![]() 到
到![]() 時兩點都停止運動,則點
時兩點都停止運動,則點![]() 的運動時間
的運動時間![]() 為多少時,
為多少時,![]() 的面積
的面積![]() 最小,最小面積為多少?
最小,最小面積為多少?
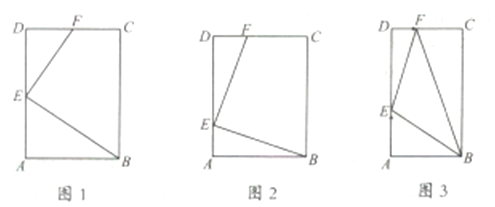
查看答案和解析>>
科目:初中數學 來源: 題型:
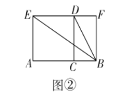
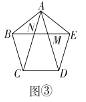
【題目】閱讀下列材料,并完成相應任務:
黃金分割
天文學家開普勒把黃金分割稱為神圣分割,并指出畢達哥拉斯定理(勾股定理)和黃金分割是幾何中的雙寶,前者好比黃金,后者堪稱珠寶,歷史上最早正式在書中使用“黃金分割”這個名稱的是歐姆,19世紀以后“黃金分割”的說法逐漸流行起來,黃金分割被廣泛應用于建筑等領域.黃金分割指把一條線段分為兩部分,使其中較長部分與線段總長之比等于較短部分與較長部分之比,該比值為![]() .用下面的方法(如圖①)就可以作出已知線段
.用下面的方法(如圖①)就可以作出已知線段![]() 的黃金分割點
的黃金分割點![]() :
:

①以線段![]() 為邊作正方形
為邊作正方形![]() ,
,
②取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
③延長![]() 到
到![]() ,使
,使![]() ,
,
④以線段![]() 為邊作正方形
為邊作正方形![]() ,點
,點![]() 就是線段
就是線段![]() 的黃金分割點.
的黃金分割點.
以下是證明點![]() 就是線段
就是線段![]() 的黃金分割點的部分過程:
的黃金分割點的部分過程:
證明:設正方形![]() 的邊長為1,則
的邊長為1,則![]() ,
,
![]() 為
為![]() 中點,
中點,
![]() ,
,
![]() 在
在![]() 中,
中,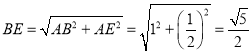 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任務:
(1)補全題中的證明過程;
(2)如圖②,點![]() 為線段
為線段![]() 的黃金分割點,分別以
的黃金分割點,分別以![]() 為邊在線段
為邊在線段![]() 同側作正方形
同側作正方形![]() 和矩形
和矩形![]() ,連接
,連接![]() .求證:
.求證:![]() ;
;
(3)如圖③,在正五邊形![]() 中,對角線
中,對角線![]() 與
與![]() 分別交于點
分別交于點![]() 求證:點
求證:點![]() 是
是![]() 的黃金分割點.
的黃金分割點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:小明為了計算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
設![]() ①
①
則![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整數,請寫出計算過程 ).
是正整數,請寫出計算過程 ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】成都市為了扎實推進精準扶貧工作,出臺了民生兜底、醫保脫貧、教育救助、產業扶持、養老托管和易地搬遷這六種幫扶措施,每戶貧困戶都享受了2到5種幫扶措施,現把享受了2種、3種、4種和5種幫扶措施的貧困戶分別稱為A,B,C,D類貧困戶,為檢查幫扶措施是否落實,隨機抽取了若干貧困戶進行調查,現將收集的數據繪制成如圖兩幅不完整的統計圖.請根據圖中信息,回答下列問題:
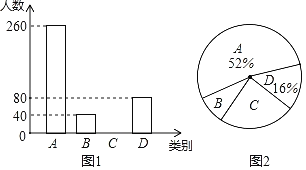
(1)本次抽樣調查了多少戶貧困戶?
(2)成都市共有9100戶貧困戶,請估計至少得到4種幫扶措施的大約有多少戶?
(3)2020年是精準扶貧攻關年,為更好地做好工作,現準備從D類貧困戶中的甲、乙、丙、丁四戶中隨機選取兩戶進行試點幫扶,請用樹狀圖或列表法求出恰好選中乙和丙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩家草莓采摘園,草莓的銷售價格相間,在生長旺季,兩家均排出優惠方案.甲園的優惠方案是:采摘的草莓不超過![]() 時,按原價銷售;若超過
時,按原價銷售;若超過![]() 超過部分
超過部分![]() 折優惠;乙園的優惠方案是:游客進園需購買
折優惠;乙園的優惠方案是:游客進園需購買![]() 元門票.采摘的草莓直接按降價出售.已知在甲園、乙園采摘草莓
元門票.采摘的草莓直接按降價出售.已知在甲園、乙園采摘草莓![]() 時,所需費用相同.
時,所需費用相同.
在乙采摘園所需費用![]() ( 元)與草梅采摘量
( 元)與草梅采摘量![]() (千克)滿足一次函數關系,如下表:
(千克)滿足一次函數關系,如下表:
數量 |
|
|
|
| ··· |
費用 |
|
|
|
| ··· |
(1)求![]() 與
與![]() 的函數關系式(不必寫出
的函數關系式(不必寫出![]() 的范圍);
的范圍);
(2)求兩個采摘園的草莓在生長旺季前的銷售價格.并求在甲采摘園所需費用![]() (元)與草莓采摘量
(元)與草莓采摘量![]() (千克)的函數關系式
(千克)的函數關系式![]() ;
;
(3)若嘉琪準備花費![]() 元去采摘草莓,去哪個園采摘,可以得到更多數量的草莓? 說明理由.
元去采摘草莓,去哪個園采摘,可以得到更多數量的草莓? 說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司計劃購買A,B兩種型號的機器人搬運材料.已知A型機器人比B型機器人每小時多搬運30kg材料,且A型機器人搬運1000kg材料所用的時間與B型機器人搬運800kg材料所用的時間相同.
(1)求A,B兩種型號的機器人每小時分別搬運多少材料;
(2)該公司計劃采購A,B兩種型號的機器人共20臺,要求每小時搬運材料不得少于2800kg,則至少購進A型機器人多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com