
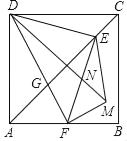
【題目】如圖,正方形ABCD中,AD=8,點E是對角線AC上一點,連接DE,過點E作EF⊥ED,交AB于點F,連接DF,交AC于點G,將△EFG沿EF翻折,得到△EFM,連接DM,交EF于點N,若點F是AB的中點,則(1)FM=_____;(2)tan∠MDE=_____.
【答案】![]()
![]()
【解析】
(1)如圖,過E作EP⊥AP,EQ⊥AD,根據(jù)正方形的性質得到∠EAQ=∠EAP=45°,推出四邊形APEQ是正方形,根據(jù)全等三角形的性質得到DE=EF,DQ=FP,且AP=EP,設EP=x,則DQ=8-x=FP=x-4,根據(jù)勾股定理得到AE=![]() ,DE=
,DE=![]() ,根據(jù)相似三角形的性質得到
,根據(jù)相似三角形的性質得到![]() =2,過G作GH⊥AB,過M作MK⊥AB,過M作ML⊥AD,根據(jù)勾股定理得到結論;
=2,過G作GH⊥AB,過M作MK⊥AB,過M作ML⊥AD,根據(jù)勾股定理得到結論;
(2)推出DM在正方形對角線DB上,過M作MK⊥AB,過N作NI⊥AB,則BK=MK=![]() ,根據(jù)平行線分線段成比例定理得到
,根據(jù)平行線分線段成比例定理得到![]() ,求得FI=4-y=1,于是得到結論.
,求得FI=4-y=1,于是得到結論.
(1)如圖,過E作EP⊥AP,EQ⊥AD,
∵四邊形APEQ是正方形,
∴DC∥AB,
∴△DGC∽△FGA,
∴![]() =2,
=2,
∵AC=8![]() ,DF=4
,DF=4![]()
∴CG=![]() ,
,
∴EG=![]() =
=![]() ,
,
AG=![]() AC=
AC=![]() ,
,
過G作GH⊥AB,過M作MK⊥AB,過M作ML⊥AD,

則易證△GHF≌△FKM全等,
∴GH=FK=![]() ,HF=MK=
,HF=MK=![]() ,
,
∴FM=![]() ;
;
∵ML=AK=AF+FK=4+![]() =
=![]() ,DL=AD-MK=8-
,DL=AD-MK=8-![]() =
=![]() ,
,
即DL=LM,
∴∠LDM=45°
∴DM在正方形對角線DB上,
過N作NI⊥AB,則NI=IB,
設NI=y,
∵NI∥EP
∴![]() ,
,
∴![]() ,
,
解得y=3,
所以FI=4-y=1,
∴I為FP的中點,
∴N是EF的中點,
∴EN=![]() EF=
EF=![]() ,
,
∵DF=4![]() ,
,
∴DE=2![]() ,
,
∴tan∠MDE=![]() ,
,
故答案為:![]() ,
,![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,正八邊形ABCDEFGH的邊長為a,I、J、K、L分別是各自所在邊的中點,且四邊形IJKL是正方形,則正方形IJKL的邊長為________(用含a的代數(shù)式表示).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖將小球從斜坡的O點拋出,小球的拋出路線可以用二次函數(shù)y=ax2+bx刻畫,頂點坐標為(4,8),斜坡可以用y=![]() x刻畫.
x刻畫.
(1)求二次函數(shù)解析式;
(2)若小球的落點是A,求點A的坐標;
(3)求小球飛行過程中離坡面的最大高度.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知一元二次方程ax2+bx+c=0兩根為x1,x2,x2+x1=﹣![]() ,x2.x1=
,x2.x1=![]() .如果拋物線y=ax2+bx+c經過點(1,2),若abc=4,且a≥b≥c,則|a|+|b|+|c|的最小值為( )
.如果拋物線y=ax2+bx+c經過點(1,2),若abc=4,且a≥b≥c,則|a|+|b|+|c|的最小值為( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
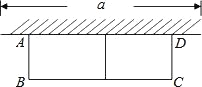
【題目】如圖,有長為 24m 的籬笆,現(xiàn)一面利用墻(墻的最大可用長度 a 為 10m)圍成中間隔有一道籬笆的長方形花圃,設花圃的寬 AB 為 xm,面積為 Sm2.
(1) 求 S 與 x 的函數(shù)關系式及 x 值的取值范圍;
(2) 要圍成面積為 45m2 的花圃,AB 的長是多少米?
(3) 當 AB 的長是多少米時,圍成的花圃的面積最大?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在成都地鐵6號線某站通道的建設中,建設工人將坡長為10米(AB=10米),坡角60°(∠BAE=60°)的斜坡通道改造成坡角為45°(∠BDE=45°)的斜坡通道,使斜坡的起點從點A處向左平移至點D處,求截面圖上AD的長.(結果保留根號).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】國家規(guī)定“中小學生每天在校體育活動時間不低于1小時”.為此,某市就“你每天在校體育活動時間是多少”的問題隨機調查了轄區(qū)內300名初中學生.根據(jù)調查結果繪制成的統(tǒng)計圖(部分)如圖所示,其中分組情況是:
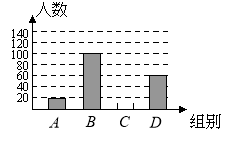
A組:![]() ;B組:
;B組:![]()
C組:![]() D組:
D組:![]()
請根據(jù)上述信息解答下列問題:
(1)C組的人數(shù)是;
(2)本次調查數(shù)據(jù)的中位數(shù)落在組內;
(3)若該轄區(qū)約有24 000名初中學生,請你估計其中達國家規(guī)定體育活動時間的人約有多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+2與x軸相交于A(﹣1,0),B(4,0)兩點,與y軸相交于點C.
(1)求拋物線的解析式;
(2)將△ABC繞AB中點M旋轉180°,得到△BAD.
①求點D的坐標;
②判斷四邊形ADBC的形狀,并說明理由;
(3)在該拋物線對稱軸上是否存在點P,使△BMP與△BAD相似?若存在,請求出所有滿足條件的P點的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小清為班級辦黑板報時遇到一個難題,在版面設計過程中需要將一個半圓三等分,小華幫他設計了一個尺規(guī)作圖的方法.
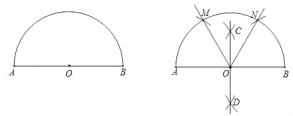
小華的作法如下:
(1)作AB的垂直平分線CD交AB于點O;
(2)分別,以A、B為圓心,以AO(或BO)的長為半徑畫弧,分別交半圓于點M、N;
(3)連接OM、ON即可
請根據(jù)該同學的作圖方法完成以下推理:
∵半圓AB
∴ 是直徑.
∵CD是線段AB的垂直平分線
∴OA=OB(依據(jù): )
∵OA=OM=
∴△OAM為等邊三角形(依據(jù): )
∴∠AOM=60°(依據(jù): )
同理可得∠BON=60°
∠AOM=∠BON=∠MON=60°
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com