【題目】(1)若a是(－4)2的平方根，b的一個平方根是2，求式子a＋b的立方根；
(2)實數a，b互為相反數，c，d互為倒數，x的絕對值為
，求式子x2＋(a＋b＋cd)x＋
＋
的值．
【答案】(1) 2或0; (2) 8＋
,8－
.
【解析】試題分析:（1）根據題意求得a、b的值，再求得a+b的值，從而求得a＋b的立方根；（2）由a，b互為相反數，c，d互為倒數，x的絕對值為
，可得a+b=0，cd=1，x=
，再代入代數式求值即可.
試題解析:
(1)依題意得a＝±4，b＝4，所以a＋b＝4＋4＝8或a＋b＝－4＋4＝0，所以a＋b的立方根是2或0.
(2)因為實數a，b互為相反數，所以a＋b＝0.因為c，d互為倒數，所以cd＝1.因為x的絕對值為
，所以x為±.
當x＝時，x2＋(a＋b＋cd)x＋
＋
＝7＋＋0＋1＝8＋.
當x＝－時，x2＋(a＋b＋cd)x＋＋＝7－＋0＋1＝8－.
科目：初中數學 來源： 題型：
【題目】閱讀材料
小明遇到這樣一個問題：求計算
所得多項式的一次項系數．
小明想通過計算
所得的多項式解決上面的問題，但感覺有些繁瑣，他想探尋一下，是否有相對簡潔的方法．
他決定從簡單情況開始，先找
所得多項式中的一次項系數．通過觀察發現：
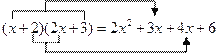
也就是說，只需用
中的一次項系數1乘以
中的常數項3，再用
中的常數項2乘以
中的一次項系數2，兩個積相加
，即可得到一次項系數．
延續上面的方法，求計算
所得多項式的一次項系數．可以先用
的一次項系數1， 
的常數項3， 
的常數項4，相乘得到12；再用
的一次項系數2， 
的常數項2， 
的常數項4，相乘得到16；然后用
的一次項系數3， 
的常數項2， 
的常數項3，相乘得到18．最后將12，16，18相加，得到的一次項系數為46．
參考小明思考問題的方法，解決下列問題：
（1）計算
所得多項式的一次項系數為 ．
（2）計算
所得多項式的一次項系數為 ．
（3）若計算
所得多項式的一次項系數為0，則
=_________．
（4）若
是
的一個因式，則
的值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A、B在反比例函數y=
的圖象上，過點A、B作x軸的垂線，垂足分別是M、N，射線AB交x軸于點C，若OM=MN=NC，四邊形AMNB的面積是3，則k的值為（ ）
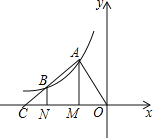
A．2 B．4 C．﹣2 D．﹣4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】推理填空：如圖，已知∠B＝∠CGF，∠DGF＝∠F，求證∠B＋∠F＝180°.
證明：∵∠B= (已知)，
∴AB∥C( )，
∵∠DGF= (已知)，
∴CD∥EF( )，
∴AB∥ ( )
∴∠B+ =180°( ).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下表所示為裝運、銷售甲、乙、丙三種蔬菜的重量及利潤。某公司計劃用20輛汽車裝運甲、乙、丙三種蔬菜共36噸到某地銷售.規定每輛汽車滿載，每車只裝一種蔬菜，每種蔬菜不少于一車。應如何安排，可使公司獲得利潤18300元?
甲 | 乙 | 丙 | |
每輛汽車裝運的噸數 | 2 | 1 | 1.5 |
每噸蔬菜可獲利潤（百元） | 5 | 7 | 4 |
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖， 
ABC的中線AD、BE相交于點F，下列結論正確的有 （ ）
①S△ABD=S△DCA；② S△AEF=S△BDF；③S四邊形EFDC=2S△AEF；④S△ABC=3S△ABF
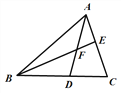
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在方格紙內將△ABC水平向右平移4個單位得到△A′B′C′．
（1）補全△A′B′C′，利用網格點和直尺畫圖；
（2）圖中AC與A1C1的關系是：______；
（3）畫出△ABC中AB邊上的中線CE；
（4）平移過程中，線段AC掃過的面積是_________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把下列各數填入相應的括號內
-π， 
，3.1， 
，0.8080080008...(相鄰兩個8之間0的個數逐次增加1)， 
-
， 
， 
， 
整數集合｛ ｝
負分數集合｛ …｝
正數集合｛ …｝
負數集合｛ …｝
有理數集合｛ …｝
無理數集合｛ …｝
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，D、E分別在邊AB、AC上，DE∥BC．
（1）試問△ADE是否是等腰三角形，并說明理由.
（2）若M為DE上的點，且BM平分
，CM平分
，若
的周長為20，BC=8.求
的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com