Question

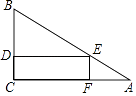
【題目】一塊三角形材料如圖所示，∠A=30°，∠C=90°，AB=12，用這塊材料剪出一個矩形CDEF，其中D、E、F分別在BC、AB、AC上．
（1）若設AE=x，則AF=；（用含x的代數式表示）
（2）要使剪出的矩形CDEF的面積最大，點E應選在何處？

Answer 1

【答案】
（1） x
（2）解：∵四邊形CDEF是矩形，

∴∠AFE=90°，

∵∠A=30°，

∴EF= AE= x，

在Rt△ABC中，∠C=90°，AB=12，

∴BC= AB=6，

根據勾股定理得：AC= =6 ，

∴CF=AC﹣AF=6 ﹣ x，

∴S矩形CDEF=CFEF= x（6 ﹣ x）=﹣ （x﹣6）2+9 ，

∴當x=6時，矩形CDEF的面積最大，

即當點E為AB的中點時，矩形CDEF的面積最大．

【解析】解：（1）在Rt△ABC中，∠A=30°，∠C=90°，AE=x， ∴EF= x，根據勾股定理得：AF= x；所以答案是： x；
【考點精析】根據題目的已知條件，利用二次函數的最值和矩形的性質的相關知識可以得到問題的答案，需要掌握如果自變量的取值范圍是全體實數，那么函數在頂點處取得最大值（或最小值），即當x=-b/2a時，y最值=(4ac-b2)/4a；矩形的四個角都是直角，矩形的對角線相等．