【題目】方程
的根可視為函數
的圖象與函數
的圖象交點的橫坐標，則方程
的實根x0所在的范圍是（ ）
A.
B.
C.
D.
【答案】C
【解析】
首先根據題意推斷方程x3+2x-1=0的實根是函數y=x2+2與
的圖象交點的橫坐標，再根據四個選項中x的取值代入兩函數解析式，找出拋物線的圖象在反比例函數上方和反比例函數的圖象在拋物線的上方兩個點即可判定推斷方程x3+2x-1=0的實根x所在范圍．
解：依題意得方程
的實根是函數
與的圖象交點的橫坐標，這兩個函數的圖象如圖所示，它們的交點在第一象限．
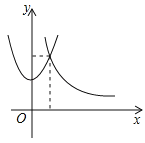
當x=
時，
，
，此時拋物線的圖象在反比例函數下方；
當x=
時，
，
，此時拋物線的圖象在反比例函數下方；
當x=
時，
，
，此時拋物線的圖象在反比例函數上方；
當x=1時，
，
，此時拋物線的圖象在反比例函數上方．
∴方程的實根x0所在范圍為：
．
故選C．
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，我們不妨把橫坐標和縱坐標相等的點叫“相等點”，例如點
，
都是“相等點”，顯然“相等點”有無數個．
（1）若點
是反比例函數
為常數，
)的圖象上的“相等點”，求這個反比例函數的解析式；
（2）一次函數
為常數，
)的圖象上存在“相等點”嗎？若存在，請用含
的式子表示出“相等點”的坐標，若不存在，說明理由；
（3）若二次函數
為常數)的圖象上有且只有一個“相等點”，令
當
時，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
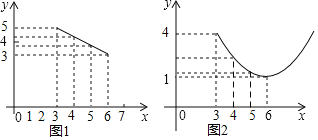
【題目】某種蔬菜每千克售價y1（元）與銷售月份x之間的關系如圖1所示，每千克成本y2（元）與銷售月份x之間的關系如圖2所示，其中圖1中的點在同一條線段上，圖2中的點在對稱軸平行于y軸的同一條拋物線上，且拋物線的最低點的坐標為(6，1)．
（1）求出y1與x函數關系式；
（2）求出y2與x函數關系式；
（3）設這種蔬菜每千克收益為w元，試問在哪個月份出售這種蔬菜，w將取得最大值？并求出此最大值．（收益＝售價﹣成本）
查看答案和解析>>
科目：初中數學 來源： 題型：
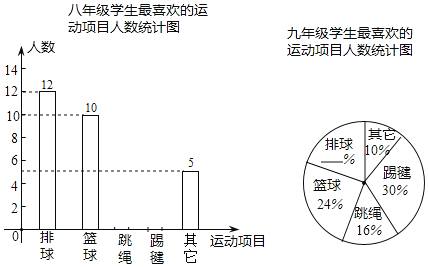
【題目】通遼市某中學為了了解學生“大課間”活動情況，在七、八、九年級的學生中，分別抽取了相同數量的學生對“你最喜歡的運動項目”進行調查（每人只能選一項），調查結果的部分數據如下表（圖）所示，其中七年級最喜歡跳繩的人數比八年級多5人，九年級最喜歡排球的人數為10人．
七年級學生最喜歡的運動項目人數統計表
項目 | 排球 | 籃球 | 踢毽 | 跳繩 | 其他 |
人數（人） | 7 | 8 | 14 |
| 6 |
請根據以上統計表（圖）解答下列問題：
（1）本次調查共抽取了多少人？
（2）補全統計表和統計圖．
（3）該校有學生1800人，學校想對“最喜歡踢毽子”的學生每4人提供一個毽子，學校現有124個毽子，能否夠用？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】每年的6月5日為世界環保日，為了提倡低碳環保，某公司決定購買10臺節省能源的新設備，現有甲、乙兩種型號的設備可供選購，經調查：購買3臺甲型設備比購買2臺乙型設備多花16萬元，購買2臺甲型設備比購買3臺乙型設備少花6萬元．
（1）求甲、乙兩種型號設備的價格；
（2）該公司經預算決定購買節省能源的新設備的資金不超過110萬元，你認為該公司有哪幾種購買方案；
（3）在（2）的條件下，已知甲型設備的產量為240噸/月，乙型設備的產量為180噸/月，若每月要求總產量不低于2040噸，為了節約資金，請你為該公司設計一種最省錢的購買方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
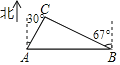
【題目】如圖，從A城市到B城市要翻過一座大山，現需要打通隧道，修建高鐵方便兩地出行，已知在A城市的北偏東30°方向和B城市的北偏西67°方向有一C地，A，C相距230km，求A，B兩個城市之間的距離．（參考數據：sin67°≈
，cos67°≈
，tan67°≈
，
≈1.7，結果精確到1km）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場準備采購一批特色商品，經調查，用5000元采購
型商品的件數是用2000元采購
型商品的件數的2倍，一件型商品的進價比一件型商品的進價多10元．
（1）求一件，型商品的進價分別為多少元？
（2）若該商場購進，型商品共200件進行試銷，其中型商品的件數不大于型商品的件數，且不小于80件．已知型商品的售價為80元/件，型商品的售價為60元/件，且，型商品均全部售出．設購進型商品
件，求該商場銷售完這批商品的利潤
與之間的函數關系式，并寫出的取值范圍；
（3）在（2）的條件下，商場決定在試銷活動中每售出一件型商品，就從一件型商品的利潤中捐獻慈善資金
元
，若該商場售完、型所有商品并捐獻資金后獲得的最大收益是4800元，求出值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有
四張不透明的卡片，除正面上的圖案不同外，其他均相同，將這四張卡片背 面向上洗勻后放在桌面上．
（1）從中隨機取出一張卡片，卡片上的圖案是中心對稱圖形的概率是_____；
（2）若從四張卡片中隨機拿出兩張卡片，請用畫樹狀圖或列表的方法，求抽取的兩張卡片都是軸對稱圖形的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
