
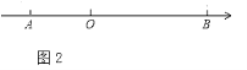
【題目】已知數軸上兩點![]() ,
,![]() 對應的數分別為
對應的數分別為![]() ,8.
,8.
(1)如圖1,如果點![]() 和點
和點![]() 分別從點
分別從點![]() ,
,![]() 同時出發,沿數軸負方向運動,點
同時出發,沿數軸負方向運動,點![]() 的運動速度為每秒2個單位,點
的運動速度為每秒2個單位,點![]() 的運動速度為每秒6個單位.
的運動速度為每秒6個單位.

①![]() ,
,![]() 兩點之間的距離為__________.
兩點之間的距離為__________.
②當![]() ,
,![]() 兩點相遇時,點
兩點相遇時,點![]() 在數軸上對應的數是____________.
在數軸上對應的數是____________.
③求點![]() 出發多少秒后,與點
出發多少秒后,與點![]() 之間相距4個單位長度?
之間相距4個單位長度?
(2)如圖2,如果點![]() 從點
從點![]() 出發沿數軸的正方向以每秒2個單位的速度運動,點
出發沿數軸的正方向以每秒2個單位的速度運動,點![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 的中點,在運動過程中,線段
的中點,在運動過程中,線段![]() 的長度是否為定值.如果變化,請說明理由:如果不變,請直接寫出線段
的長度是否為定值.如果變化,請說明理由:如果不變,請直接寫出線段![]() 的長度.
的長度.
【答案】(1)①![]() 兩點之間的距離為12,②當
兩點之間的距離為12,②當![]() ,
,![]() 兩點相遇時,點
兩點相遇時,點![]() 在數軸上對應的數是
在數軸上對應的數是![]() ,③2秒;(2)不變,
,③2秒;(2)不變,![]() ,見解析.
,見解析.
【解析】
(1)①根據兩點間的距離公式即可求解;
②根據相遇時間=路程差÷速度差先求出時間,再根據路程=速度×時間求解即可;
③分兩種情況:P,Q兩點相遇前;P,Q兩點相遇后;進行討論即可求解;
(2)由線段中點的性質可求MN的值不變.
(1)①A,B兩點之間的距離為8-(-4)=12.
②12÷(6-2)=3(秒),
-4-2×3=-10.
故當P,Q兩點相遇時,點P在數軸上對應的數是-10.
③P,Q兩點相遇前,
(12-4)÷(6-2)=2(秒),
P,Q兩點相遇后,
(12+4)÷(6-2)=4(秒).
故求點P出發2或4秒后,與點Q之間相距4個單位長度;
(2)線段MN的長度不會變化,
∵點M為PA的中點,點N為PB的中點,
∴PM=![]() PA,PN=
PA,PN=![]() PB
PB
∴PM+PN=![]() (PA+PB)
(PA+PB)
∴MN=![]() AB=6
AB=6


科目:初中數學 來源: 題型:
【題目】仔細閱讀下面例題,解答問題:
例題:已知二次三項式x2-4x+m有一個因式是(x+3),求另一個因式以及m的值.
解:設另一個因式為(x+n),得x2-4x+m=(x+3)(x+n),則x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得:![]() .
.
∴另一個因式為(x-7),m的值為-21.
問題:仿照以上方法解答下面問題:
(1)已知二次三項式2x2+3x-k有一個因式是(2x-5),求另一個因式以及k的值
(2)已知二次三項式6x2+4ax+2有一個因式是(2x+a),a是正整數,求另一個因式以及a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面推理過程:
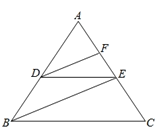
如圖,已知:DE∥BC,DF、BE分別平分∠ADE、∠ABC.
求證:∠FDE=∠DEB
證明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分別平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ ③ ( ④ )
∠ ③ ( ④ )
∠ABE=![]() ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )
∴∠ADF=∠ABE(等量代換)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
查看答案和解析>>
科目:初中數學 來源: 題型:
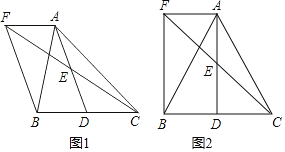
【題目】如圖1,在△ABC中,D是BC邊上一點,E是AD的中點,過點A作BC的平行線交CE的延長線于F,且AF=BD,連接BF.
(1)求證:點D是線段BC的中點;
(2)如圖2,若AB=AC=13,AF=BD=5,求四邊形AFBD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗中學地理社團學生在5名地理老師的帶領下去黃河風景區進行參觀考察,景區的門票為每人40元.現有兩種優惠方案.甲方案:帶隊教師免費,學生按9折收費;乙方案:師生都8折收費.
(1)若有![]() 名學生,用代數式表示兩種優惠方案各需多少元?
名學生,用代數式表示兩種優惠方案各需多少元?
(2)當![]() 為何值時,兩種優惠方案收費相同?
為何值時,兩種優惠方案收費相同?
(3)當![]() 時,采用哪種方案優惠?
時,采用哪種方案優惠?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有依次3個數:2、9、7.對任意相鄰的兩個數,都用右邊的數減去左邊的數,所得之差寫在這兩個數之間,可產生一個新數串:2、7、9、-2、7,這稱為第1次操作,做第2次同樣的操作后也可以產生一個新數串:2、5、7、2、9、-11、-2、9、7,繼續依次操作下去,問從數串2、9、7開始操作第20次后所產生的那個數串的所有數之和是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=6,AC=10,∠BAC和∠ACB的平分線相交于點E,過點E作EF∥BC交AC于點F,那么EF的長為( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164379648/STEM/8dc0999226e6439d82d3fa2c2424ef2e.png]
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長均為1個單位的正方形網格圖中,建立了平面直角坐標系xOy,按要求解答下列問題:

(1)寫出△ABC三個頂點的坐標;
(2)畫出△ABC向右平移6個單位后得到的圖形△A1B1C1;
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定理描述
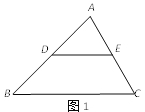
(1)如圖1,用文字語言或符號語言敘述三角形中位線性質定理的內容.
.
證法回顧
證明三角形中位線性質定理的方法很多,但多數都需要通過添加輔助線構圖去完成.下列是其中一種證法的添加輔助線方法:
添加輔助線,如圖2,在△ABC中,過點C作CF∥AB,與DE的延長線交于點F.
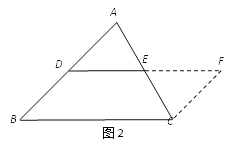
(2)上述證法中,證明三角形中位線定理中的DE∥BC的依據是( )
A.同位角相等,兩直線平行.
B.平行四邊形對邊平行.
C.同旁內角互補,兩直線平行.
D.平行于同一條直線的兩條直線互相平行
拓展延伸
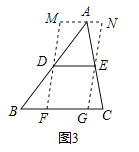
(3)利用證明三角形中位線定理獲得的經驗解決下面的問題:
如圖3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位線,過點D、E作DF∥EG,分別交BC于F、G,過點A作MN∥BC,分別與FD、GE的延長線交于M、N,則四邊形MFGN周長的最小值是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com