
【題目】已知二次函數(shù)![]() 與一次函數(shù)
與一次函數(shù)![]() 的圖象交點(diǎn)為
的圖象交點(diǎn)為![]() ,
,![]() ,且二次函數(shù)的最小值為
,且二次函數(shù)的最小值為![]() ,則這個(gè)二次函數(shù)的解析式為________.
,則這個(gè)二次函數(shù)的解析式為________.
【答案】![]() 或
或![]()
【解析】
根據(jù)題意設(shè)二次函數(shù)的解析式為:y=a(x-k)2+1,然后把(-1,2),(2,5)代入解析式得,得到2=a(-1-k)2+1①,5=a(2-k)2+1②,解由①②組成的方程組得,k=0,a=1或k=-4,a=![]() 即得到二次函數(shù)的解析式.
即得到二次函數(shù)的解析式.
設(shè)二次函數(shù)的解析式為:y=a(x-k)2+1,
把(-1,2),
(2,5)代入解析式,
得2=a(-1-k)2+1①,
5=a(2-k)2+1②,
解由①②組成的方程組得,k=0,a=1或k=-4,a=![]() ;
;
∴二次函數(shù)的解析式為y=x2+1或y=![]() (x+4)2+1=
(x+4)2+1=![]() x2+
x2+![]() .
.
故答案為:y=x2+1或y=![]() .
.


 七彩題卡口算應(yīng)用一點(diǎn)通系列答案
七彩題卡口算應(yīng)用一點(diǎn)通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在“雙十二”期間,A,B兩個(gè)超市開展促銷活動(dòng),活動(dòng)方式如下:
A超市:購物金額打9折后,若超過2000元再優(yōu)惠300元;
B超市:購物金額打8折.
某學(xué)校計(jì)劃購買某品牌的籃球做獎(jiǎng)品,該品牌的籃球在A,B兩個(gè)超市的標(biāo)價(jià)相同.根據(jù)商場(chǎng)的活動(dòng)方式:
(1)若一次性付款4200元購買這種籃球,則在B商場(chǎng)購買的數(shù)量比在A商場(chǎng)購買的數(shù)量多5個(gè).請(qǐng)求出這種籃球的標(biāo)價(jià);
(2)學(xué)校計(jì)劃購買100個(gè)籃球,請(qǐng)你設(shè)計(jì)一個(gè)購買方案,使所需的費(fèi)用最少.(直接寫出方案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°.
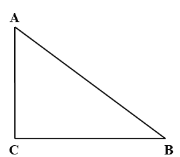
(1)作∠BAC的平分線,交BC于點(diǎn)D;(要求:尺規(guī)作圖,不寫作法,保留作圖痕跡)
(2)在(1)的條件下,若BD=5,CD=3,求AC的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)解方程:![]() ;
;
(2)列分式方程解應(yīng)用題:
用電腦程序控制小型賽車進(jìn)行![]() 比賽,“暢想號(hào)”和“逐夢(mèng)號(hào)”兩賽車進(jìn)入了最后的決賽.比賽中,兩車從起點(diǎn)同時(shí)出發(fā),“暢想號(hào)”到達(dá)終點(diǎn)時(shí),“逐夢(mèng)號(hào)”離終點(diǎn)還差
比賽,“暢想號(hào)”和“逐夢(mèng)號(hào)”兩賽車進(jìn)入了最后的決賽.比賽中,兩車從起點(diǎn)同時(shí)出發(fā),“暢想號(hào)”到達(dá)終點(diǎn)時(shí),“逐夢(mèng)號(hào)”離終點(diǎn)還差![]() .從賽后數(shù)據(jù)得知兩車的平均速度相差
.從賽后數(shù)據(jù)得知兩車的平均速度相差![]() .求“暢想號(hào)”的平均速度.
.求“暢想號(hào)”的平均速度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】把拋物線![]() 沿
沿![]() 軸向右平移
軸向右平移![]() 個(gè)單位后,再沿
個(gè)單位后,再沿![]() 軸翻折得到拋物線
軸翻折得到拋物線![]() 稱為第一次操作,把拋物線
稱為第一次操作,把拋物線![]() 沿
沿![]() 軸向右平移
軸向右平移![]() 個(gè)單位后,再沿
個(gè)單位后,再沿![]() 軸翻折得到拋物線
軸翻折得到拋物線![]() 稱為第二次操作,…,以此類推,則拋物線
稱為第二次操作,…,以此類推,則拋物線![]() 經(jīng)過第
經(jīng)過第![]() 此操作后得到的拋物線
此操作后得到的拋物線![]() 的解析式為( )
的解析式為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),![]() 點(diǎn)在原點(diǎn)的左側(cè),
點(diǎn)在原點(diǎn)的左側(cè),![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() ,與
,與![]() 軸交于
軸交于![]() 點(diǎn),點(diǎn)
點(diǎn),點(diǎn)![]() 是直線
是直線![]() 下方的拋物線上一動(dòng)點(diǎn).
下方的拋物線上一動(dòng)點(diǎn).
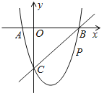
![]() 求這個(gè)二次函數(shù)的表達(dá)式.
求這個(gè)二次函數(shù)的表達(dá)式.
![]() 連接
連接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四邊形
翻折,得到四邊形![]() ,那么是否存在點(diǎn)
,那么是否存在點(diǎn)![]() ,使四邊形
,使四邊形![]() 為菱形?若存在,請(qǐng)求出此時(shí)點(diǎn)
為菱形?若存在,請(qǐng)求出此時(shí)點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
![]() 當(dāng)點(diǎn)
當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到什么位置時(shí),四邊形
運(yùn)動(dòng)到什么位置時(shí),四邊形![]() 的面積最大?求出此時(shí)
的面積最大?求出此時(shí)![]() 點(diǎn)的坐標(biāo)和四邊形
點(diǎn)的坐標(biāo)和四邊形![]() 的最大面積.
的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
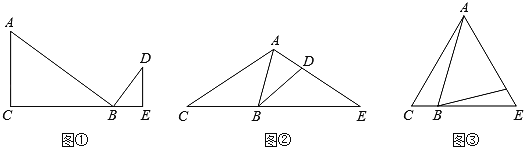
【題目】已知,點(diǎn)B在線段CE上.
(感知)(1)如圖①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求證明);
(拓展)(2)如圖②,△ACE中,AC=AE,且∠ABD=∠E,求證:△ACB∽△BED;
(應(yīng)用)(3)如圖③,△ACE為等邊三角形,且∠ABD=60°,AC=6,BC=2,則△ABD與△BDE的面積比為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
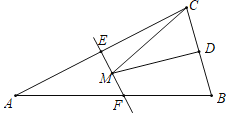
【題目】如圖,等腰三角形ABC的底邊BC長(zhǎng)為6,面積是18,腰AC的垂直平分線EF分別交AC,AB于E,F點(diǎn),若點(diǎn)D為BC邊的中點(diǎn),點(diǎn)M為線段EF上一動(dòng)點(diǎn),則△CDM的周長(zhǎng)的最小值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
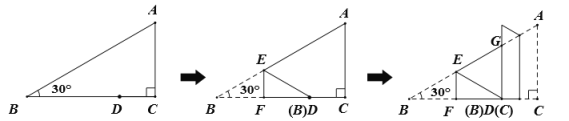
【題目】在三角形紙片![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() (不與
(不與![]() ,
,![]() 重合)是
重合)是![]() 上任意一點(diǎn),將此三角形紙片按下列方式折疊,若
上任意一點(diǎn),將此三角形紙片按下列方式折疊,若![]() 的長(zhǎng)度為
的長(zhǎng)度為![]() ,則
,則![]() 的周長(zhǎng)為__________.(用含
的周長(zhǎng)為__________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com