
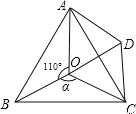
【題目】如圖,點O是等邊△ABC內一點,∠AOB=110°,∠BOC=a.將△BOC繞點C按順時針方向旋轉60°得△ADC,連接OD.
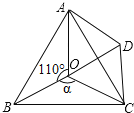
(1)求證:△COD是等邊三角形;
(2)當a=150°時,試判斷△AOD的形狀,并說明理由;
(3)探究:當a為多少度時,△AOD是等腰三角形?
【答案】(1)證明見解析;(2)當α=150°時,△AOD是直角三角形,理由見解析;(3)當α的度數為125°或110°或140°時,△AOD是等腰三角形.
【解析】試題分析:(1)根據旋轉的性質可得出![]() ,結合題意即可證得結論;
,結合題意即可證得結論;
(2)結合(1)的結論可作出判斷;
(3)找到變化中的不變量,然后利用旋轉及全等的性質即可做出解答.
試題解析:(1)證明:∵將△BOC繞點C按順時針方向旋轉![]() 得△ADC,
得△ADC,
∴CO=CD,∠OCD=![]() ,
,
∴△COD是等邊三角形,
(2)當![]() 時,△AOD是直角三角形.
時,△AOD是直角三角形.
理由是:∵將△BOC繞點C按順時針方向旋轉60![]() 得△ADC,
得△ADC,
∴△BOC≌△ADC,
![]()
又∵△COD是等邊三角形,
∴∠ODC=![]() ,
,
![]()
![]()
![]()
∴△AOD不是等腰直角三角形,即△AOD是直角三角形。
(3)①要使AO=AD,需∠AOD=∠ADO,
![]()
![]()
![]()
②要使OA=OD,需∠OAD=∠ADO.
![]()
![]()
![]()
③要使OD=AD,需∠OAD=∠AOD.
![]()
![]()
![]()
解得![]()
綜上所述:當α的度數為![]() 或
或![]() 或
或![]() 時,△AOD是等腰三角形。
時,△AOD是等腰三角形。


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
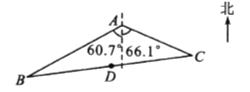
【題目】如圖,濕地景區岸邊有三個觀景臺![]() 、
、![]() 、
、![]() .已知
.已知![]() m,
m, ![]() m,點
m,點![]() 位于點
位于點![]() 的南偏西60. 7°方向,點
的南偏西60. 7°方向,點![]() 位于點
位于點![]() 的南偏東66. 1°方向.
的南偏東66. 1°方向.
(1)求![]() 的面積;
的面積;
(2)景區規劃在線段![]() 的中點
的中點![]() 處修建一個湖心亭,并修建觀景棧道
處修建一個湖心亭,并修建觀景棧道![]() .試求
.試求![]() 、
、![]() 間的距離.(結果精確到0. 1 m,參考數據:
間的距離.(結果精確到0. 1 m,參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c的圖象過A(2,0), B(0,﹣1)和C(4,5)三點.
(1)求二次函數的解析式;
(2)設二次函數的圖象與x軸的另一個交點為D,求點D的坐標;
(3)在同一坐標系中畫出直線y=x+1,并寫出當x在什么范圍內時,一次函數的值大于二次函數的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=8,BC=6。P是AB邊上的一個動點(異于A、B兩點),過點P分別作AC、BC邊的垂線,垂足為M、N設AP=x。

(1)在△ABC中,AB= ;
(2)當x= 時,矩形PMCN的周長是14;
(3)是否存在x的值,使得△PAM的面積、△PBN的面積與矩形PMCN的面積同時相等?請說出你的判斷,并加以說明。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,點E在邊AD上(不與點A、D重合),∠CEB=45°,EB與對角線AC相交于點F,設DE=x.
(1)用含x的代數式表示線段CF的長;
(2)如果把△CAE的周長記作C△CAE,△BAF的周長記作C△BAF,設![]() =y,求y關于x的函數關系式,并寫出它的定義域;
=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當∠ABE的正切值是![]() 時,求AB的長.
時,求AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算題
(1)計算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)計算:![]()
(3)化簡:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化簡:3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,在矩形紙片
,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() .過點
.過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() ,
,![]() 也隨之移動.
也隨之移動.
①當點![]() 與點
與點![]() 重合時(如圖
重合時(如圖![]() ),求菱形
),求菱形![]() 的邊長;
的邊長;
②若限定![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上移動,求出點
上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com