
已知,如圖①,∠MON=60°,點A、B為射線OM、ON上的動點(點A、B不與點O重合),且AB= ,在∠MON的內部、△AOB的外部有一點P,且AP=BP,∠APB=120°.
,在∠MON的內部、△AOB的外部有一點P,且AP=BP,∠APB=120°.

(1)求AP的長;
(2)求證:點P在∠MON的平分線上;
(3)如圖②,點C,D,E,F(xiàn)分別是四邊形AOBP的邊AO,OB,BP,PA的中點,連接CD,DE,EF,F(xiàn)C,OP.
①當AB⊥OP時,請直接寫出四邊形CDEF的周長;
②若四邊形CDEF的周長用t表示,請直接寫出t的取值范圍.
(1)4;(2)過點P分別作PS⊥OM于點S, PT⊥ON于點T,根據四邊形的內角和定理可得∠SPT的度數,即可得到∠APS=∠BPT,再結合∠ASP=∠BTP=90°,AP=BP,即可證得△APS≌△BPT,從而證得結論;(3)①8+4 ;②4+4
;②4+4 <t≤8+4
<t≤8+4
【解析】
試題分析:(1)過點P作PQ⊥AB于點Q,先根據等腰三角形的性質求得AQ的長,∠APQ的度數,在Rt△APQ中,根據∠APQ的正弦函數即可求得結果;
(2)過點P分別作PS⊥OM于點S, PT⊥ON于點T,根據四邊形的內角和定理可得∠SPT的度數,即可得到∠APS=∠BPT,再結合∠ASP=∠BTP=90°,AP=BP,即可證得△APS≌△BPT,從而證得結論;
(3)根據三角形的中位線定理即可求得結果.
(1)過點P作PQ⊥AB于點Q
∵PA=PB,∠APB=120°,AB=4 ,
,
∴AQ= AB=
AB= ×4
×4 =2
=2 ,∠APQ=
,∠APQ= ∠APB=
∠APB= ×120°=60°
×120°=60°
在Rt△APQ中,sin∠APQ=
∴AP= =4
=4
(2)過點P分別作PS⊥OM于點S, PT⊥ON于點T

∴∠OSP=∠OTP=90°
在四邊形OSPT中,∠SPT=360°-∠OSP-∠SOT-∠OTP=360°-90°-60°-90°=120°,
∴∠APB=∠SPT=120°
∴∠APS=∠BPT
又∵∠ASP=∠BTP=90°,AP=BP,
∴△APS≌△BPT
∴PS=PT
∴點P在∠MON的平分線上;
(3)①8+4
②4+4 <t≤8+4
<t≤8+4 .
.
考點:等腰三角形的性質,正弦函數,全等三角形的判定和性質,三角形的中位線定理
點評:解答本題的關鍵是讀懂題意及圖形,正確作出輔助線,同時熟記三角形的中位線平行于第三邊,且等于第三邊的一半.


科目:初中數學 來源: 題型:
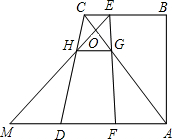 EH交AD的延長線于點M,交AC于點O,設EC=x.
EH交AD的延長線于點M,交AC于點O,設EC=x.查看答案和解析>>
科目:初中數學 來源: 題型:
 25、已知;如圖,AB是半圓O的直徑,弦CD∥AB,直線CM、DN分別切半圓于點C、D,且分別和直線AB相交于點M、N.
25、已知;如圖,AB是半圓O的直徑,弦CD∥AB,直線CM、DN分別切半圓于點C、D,且分別和直線AB相交于點M、N.查看答案和解析>>
科目:初中數學 來源: 題型:
 (1998•河北)已知:如圖,在⊙O中,直徑AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,連接MO并延長,交⊙O于N.則下列結論中,正確的是( )
(1998•河北)已知:如圖,在⊙O中,直徑AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,連接MO并延長,交⊙O于N.則下列結論中,正確的是( )查看答案和解析>>
科目:初中數學 來源: 題型:
| 4 | 5 |

查看答案和解析>>
科目:初中數學 來源:2012-2013學年上海市閘北區(qū)中考一模數學試卷(解析版) 題型:解答題
(本題滿分14分 第(1)小題4分,第(2)小題4分,第(3)小題6分)
已知:如圖,在△ABC中,AB=AC=15, cos∠A= .點M在AB邊上,AM=2MB,點P是邊AC上的一個動點,設PA=x.
.點M在AB邊上,AM=2MB,點P是邊AC上的一個動點,設PA=x.

(1)求底邊BC的長;
(2)若點O是BC的中點,聯(lián)接MP、MO、OP,設四邊形AMOP的面積是y,求y關于x的函數關系式,并出寫出x的取值范圍;
(3)把△MPA沿著直線MP翻折后得到△MPN,是否可能使△MPN的一條邊(折痕邊PM除外)與AC垂直?若存在,請求出x的值;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com