
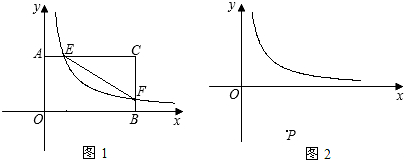
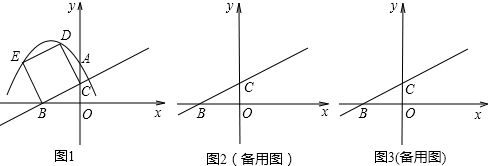
如圖1,在直角坐標系中,點A的坐標為(1,0),以OA為邊在第一象限內作正方形OABC,點D是 軸正半軸上一動點(OD>1),連結BD,以BD為邊在第一象限內作正方形DBFE,設M為正方形DBFE的中心,直線MA交
軸正半軸上一動點(OD>1),連結BD,以BD為邊在第一象限內作正方形DBFE,設M為正方形DBFE的中心,直線MA交 軸于點N.如果定義:只有一組對角是直角的四邊形叫做損矩形.
軸于點N.如果定義:只有一組對角是直角的四邊形叫做損矩形.
(1)試找出圖1中的一個損矩形;
(2)試說明(1)中找出的損矩形的四個頂點在同一個圓上;
(3)隨著點D位置的變化,點N的位置是否會發生變化?若沒有發生變化,求出點N的坐標;若發生變化,請說明理由;
(4)在圖2中,過點M作MG⊥ 軸于點G,連結DN,若四邊形DMGN為損矩形,求D點坐標.
軸于點G,連結DN,若四邊形DMGN為損矩形,求D點坐標. 
(1)四邊形ABMD為損矩形;(2)見解析;(3)(0,-1);(4)(3,0)
解析試題分析:(1)根據題中給出的損矩形的定義,從圖找出只有一組對角是直角的四邊形即可;
(2)證明四邊形BADM四個頂點到BD的中點距離相等即可;
(3)利用同弧所對的圓周角相等可得∠MAD=∠MBD,進而得到OA=ON,即可求得點N的坐標;
(4)根據正方形的性質及損矩形含有的直角,利用勾股定理求解.
(1)四邊形ABMD為損矩形;
(2)取BD中點H,連結MH,AH
∵四邊形OABC,BDEF是正方形
∴△ABD,△BDM都是直角三角形
∴HA=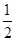 BD HM=
BD HM=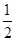 BD
BD
∴HA=HB=HM=HD=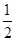 BD
BD
∴損矩形ABMD一定有外接圓
(3)∵損矩形ABMD一定有外接圓⊙H
∴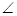 MAD =
MAD =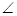 MBD
MBD
∵四邊形BDEF是正方形
∴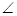 MBD=45°
MBD=45°
∴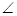 MAD=45°
MAD=45°
∴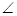 OAN=45°
OAN=45°
∵OA=1
∴ON=1
∴N點的坐標為(0,-1)
(4) 延長AB交MG于點P,過點M作MQ⊥ 軸于點Q
軸于點Q
設MG= ,則四邊形APMQ為正方形
,則四邊形APMQ為正方形
∴PM=AQ= -1 ∴OG=MQ=
-1 ∴OG=MQ= -1
-1
∵△MBP≌△MDQ
∴DQ=BP=CG= -2
-2
∴MN2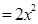
ND2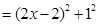
MD2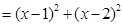
∵四邊形DMGN為損矩形
∴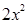
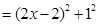
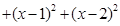
∴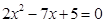
∴ =2.5或
=2.5或 =1(舍去)
=1(舍去)
∴OD=3
∴D點坐標為(3,0).
考點:本題考查的是確定圓的條件,正方形的性質
點評:解答本題的關鍵是理解損矩形的只有一組對角是直角的性質,


科目:初中數學 來源: 題型:
| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
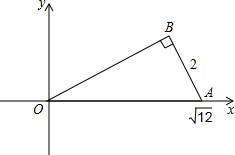 已知在Rt△OAB中,∠B=90°,AO=
已知在Rt△OAB中,∠B=90°,AO=| 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| ||||
| a+12 |

查看答案和解析>>
科目:初中數學 來源: 題型:
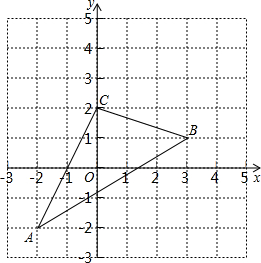 如圖,△ABC在直角坐標系中,
如圖,△ABC在直角坐標系中,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com