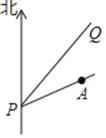
【題目】如圖，臺風中心位于
點，并沿東北方向
移動，已知臺風移動的速度為
，受影響區域的半徑為
，
市位于點的北偏東
方向上，距離點
處．
（1）市是否受到這次臺風的影響？為什么？
（2）若市受到臺風影響，求受影響的時間有多長？
【答案】(1)見解析;(2)8h.
【解析】
（1）作AB⊥PQ于點H，在Rt△ABP中，求出BH的長與200千米相比較即可；
（2）以A為圓心，以200為半徑作圓交PQ于C、D兩點，求出CD的長，再根據臺風的速度即可求出臺風影響A市的時間．
（1）
市會受到臺風影響，
如圖所示：
∵臺風中心位于點P，并沿東北方向PQ移動，A市位于點P的北偏東75°方向上，
∴∠QPG=45°，∠NPA=75°，∠APG=15°，
∴∠APQ=30°，
作AB⊥PQ于點B，在Rt△ABP中，由條件知，PA=320，
得 AB=
PA=160＜200，
∴市會受到臺風影響；
（2）如圖，以A為圓心，以200為半徑作圓交PQ于C、D兩點，若臺風中心移動到C時，臺風開始影響A市，臺風中心移動到D時，臺風影響結束．
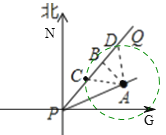
由（1）得AB=160，由條件得AC=AD=200，
由勾股定理得
=
=
，
∴CD=2CB=240，
∴臺風影響的時間t= 240÷30=8(h)，
∴A市受影響時間是8h．
名師伴你成長課時同步學練測系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC邊上的兩個動點，其中點P從點A開始沿A→B方向運動，且速度為每秒1cm，點Q從點B開始沿B→C→A方向運動，且速度為每秒2cm，它們同時出發，設出發的時間為t秒．
（1）出發2秒后，求PQ的長；
（2）當點Q在邊BC上運動時，出發幾秒鐘后，△PQB能形成等腰三角形？
（3）當點Q在邊CA上運動時，求能使△BCQ成為等腰三角形的運動時間．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】樂樂家附近的商場為了吸引顧客，設立了一個可以自由轉動的轉盤，
為轉盤直徑，如圖所示，并規定：顧客消費50元（含50元）以上，就能獲得一次轉動轉盤的機會，如果轉盤停止后，指針正好對準9折、8折、7折區域，則顧客就可以獲得相應區域的優惠.
（1）某顧客在該商場消費40元，是否可以獲得轉動轉盤的機會？
（2）某顧客在該商場正好消費66元，則他轉動一次轉盤，獲得三種打折優惠的概率分別是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我校初一某班學生的平均體重是45公斤．
（1）下表給出了該班6位同學的體重情況（單位：公斤），完成下表
姓 名 | 小麗 | 小華 | 小明 | 小方 | 小穎 | 小寶 |
體 重 | 37 | 50 | 40 |
| 36 | 48 |
體重與平均體重的差值 | ﹣8 | +5 |
| +2 |
|
|
（2）最重的與最輕的同學的體重相差多少？
（3）這6位同學的平均體重是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠1=∠2，AC=AD，增加下列條件：①AB=AE；②BC=DE；③∠C=∠D；④∠B=∠E，其中能使△ABC≌△AED的條件是______________．（填寫序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
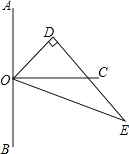
【題目】如圖，點O在直線AB上，OC⊥AB，△ODE中，∠ODE=90°，∠EOD=60°，先將△ODE一邊OE與OC重合，然后繞點O順時針方向旋轉，當OE與OB重合時停止旋轉．
（1）當OD在OA與OC之間，且∠COD=20°時，則∠AOE=______；
（2）試探索：在△ODE旋轉過程中，∠AOD與∠COE大小的差是否發生變化？若不變，請求出這個差值；若變化，請說明理由；
（3）在△ODE的旋轉過程中，若∠AOE=7∠COD，試求∠AOE的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
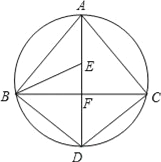
【題目】如圖，AD為△ABC外接圓的直徑，AD⊥BC，垂足為點F，∠ABC的平分線交AD于點E，連接BD，CD．
（1）求證：BD=CD；
（2）請判斷B，E，C三點是否在以D為圓心，以DB為半徑的圓上？并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
