
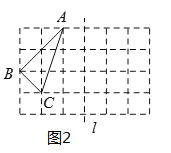
【題目】(1)如圖②,利用網格線畫![]() ,使它與
,使它與![]() 關于直線
關于直線![]() 對稱.若每個小正方形邊長為1,則
對稱.若每個小正方形邊長為1,則![]() 的面積為__.
的面積為__.
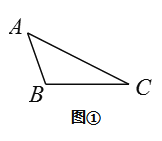
(2)如圖①,用直尺和圓規在△ABC的一邊![]() 上確定一點
上確定一點![]() ,使PC=PB.若△ABP的周長為16,BC=8,則△ABC的周長為__.
,使PC=PB.若△ABP的周長為16,BC=8,則△ABC的周長為__.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】完成下面的證明.
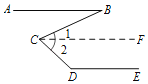
已知:如圖,AB∥DE,求證:∠D+∠BCD﹣∠B=180°.
證明:過點C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市在創建全國文明城市過程中,決定購買A,B兩種樹苗對某路段道路進行綠化改造,已知購買A種樹苗8棵,B種樹苗3棵,需要950元;若購買A種樹苗5棵,B種樹苗6棵,則需要800元.
(1)求購買A,B兩種樹苗每棵各需多少元?
(2)考慮到綠化效果和資金周轉,購進A種樹苗不能少于48棵,且用于購買這兩種樹的資金不能超過7500元,若購進這兩種樹苗共100棵,則有哪幾種購買方案?
(3)某包工隊承包種植任務,若種好一棵A種樹苗可獲工錢30元,種好一棵B種樹苗可獲工錢20元,在第(2)問的各種購買方案中,種好這100棵樹苗,哪一種購買方案所付的種植工錢最少?最少工錢是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,∠1=∠2,則不一定能使△ABD≌△ACD的條件是 ( )
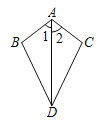
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CA⊥AB,垂足為點A,AB=8,AC=4,射線BM⊥AB,垂足為點B,一動點E從A點出發以2厘米/秒的速度沿射線AN運動,點D為射線BM上一動點,隨著E點運動而運動,且始終保持ED=CB,當點E離開點A后,運動______ 秒時,△DEB與△BCA全等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=x2+(a﹣2)x+3的圖象與一次函數y=x(1≤x≤2)的圖象有且僅有一個交點,則實數a的取值范圍是( )
A. a=3±2![]() B. ﹣1≤a<2
B. ﹣1≤a<2
C. a=3![]() 或﹣
或﹣![]() ≤a<2 D. a=3﹣2
≤a<2 D. a=3﹣2![]() 或﹣1≤a<﹣
或﹣1≤a<﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)由大小相同的小立方塊搭成的幾何體如圖1,請在圖2的方格中畫出該幾何體的俯視圖和左視圖.
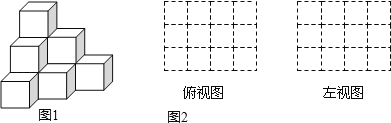
(2)用小立方體搭一個幾何體,使得它的俯視圖和左視圖與你在方格中所畫的一致,則這樣的幾何體最少要 個小立方塊,最多要 個小立方塊.
查看答案和解析>>
科目:初中數學 來源: 題型:
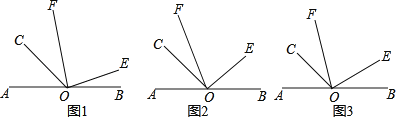
【題目】如圖,O是直線AB上的一點,∠AOC=45°,OE是∠BOC內部的一條射線,且OF平分∠AOE.
(1)如圖1,若∠COF=35°,求∠EOB的度數;
(2)如圖2,若∠EOB=40°,求∠COF的度數;
(3)如圖3,∠COF與∠EOB有怎樣的數量關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有兩個紙箱,每個紙箱內各裝有4個材質、大小都相同的乒乓球,其中一個紙箱內4個小球上分別寫有1、2、3、4這4個數,另一個紙箱內4個小球上分別寫有5、6、7、8這4個數,甲、乙兩人商定了一個游戲,規則是:從這兩個紙箱中各隨機摸出一個小球,然后把兩個小球上的數字相乘,若得到的積是2的倍數,則甲得1分,若得到積是3的倍數,則乙得2分.完成一次游戲后,將球分別放回各自的紙箱,搖勻后進行下一次游戲,最后得分高者勝出.。
(1)請你通過列表(或樹狀圖)分別計算乘積是2的倍數和3的倍數的概率;
(2)你認為這個游戲公平嗎?為什么?若你認為不公平,請你修改得分規則,使游戲對雙方公平.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com