
【題目】如圖,在同一平面上,兩塊斜邊相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜邊AC完全重合,且頂點(diǎn)B,D分別在AC的兩旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
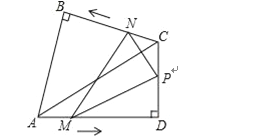
(1)填空:AD= (cm),DC= (cm)
(2)點(diǎn)M,N分別從A點(diǎn),C點(diǎn)同時(shí)以每秒1cm的速度等速出發(fā),且分別在AD,CB上沿A→D,C→B方向運(yùn)動(dòng),點(diǎn)N到AD的距離(用含x的式子表示)
(3)在(2)的條件下,取DC中點(diǎn)P,連接MP,NP,設(shè)△PMN的面積為y(cm2),在整個(gè)運(yùn)動(dòng)過(guò)程中,△PMN的面積y存在最大值,請(qǐng)求出y的最大值.
(參考數(shù)據(jù)sin75°=![]() ,sin15°=
,sin15°=![]() )
)
【答案】(1)![]() ;
;![]() ;
;
(2)![]() ;
;
(3)![]()
【解析】
試題根據(jù)直角三角形的勾股定理分別求出AD和DC的長(zhǎng)度;過(guò)點(diǎn)N作NE⊥AD于E,作NF⊥DC延長(zhǎng)線(xiàn)于F,則NE=DF,根據(jù)∠ACD=60°,∠ACB=45°得出∠NCF=75°,∠FNC=15°,設(shè)NC=x,根據(jù)sin15°的值得出FC的值,則得出NE、DF的長(zhǎng)度,從而得出點(diǎn)N到AD的距離;根據(jù)sin75°得出FN的長(zhǎng)度,根據(jù)PD和CP的長(zhǎng)度得出PF的長(zhǎng)度,從而得出y與x的函數(shù)關(guān)系式,然后根據(jù)二次函數(shù)的最值求法求出最大值.
試題解析:(1)![]() ;
;![]() ;
;
(2)如圖,過(guò)點(diǎn)N作NE⊥AD于E,作NF⊥DC延長(zhǎng)線(xiàn)于F,則NE=DF.∵∠ACD=60°,∠ACB=45°,
∴∠NCF=75°,∠FNC=15°, ∴sin15°=![]() ,又NC=x, ∴
,又NC=x, ∴![]() ,
,
∴NE=DF=![]() . ∴點(diǎn)N到AD的距離為
. ∴點(diǎn)N到AD的距離為![]() cm;
cm;
(3)∵sin75°=![]() ,∴
,∴![]() , ∵PD=CP=
, ∵PD=CP=![]() ,
,
∴PF=![]() ,
,
∴![]() ·
·![]()
即![]() ,
,
當(dāng)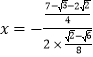 =
=![]() 時(shí),y有最大值為
時(shí),y有最大值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
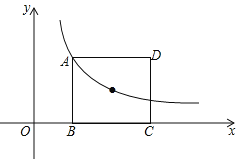
【題目】如圖,矩形ABCD的頂點(diǎn)A和對(duì)稱(chēng)中心均在反比例函數(shù)y=![]() (k≠0,x>0)上,若矩形ABCD的面積為8,則k的值為___.
(k≠0,x>0)上,若矩形ABCD的面積為8,則k的值為___.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
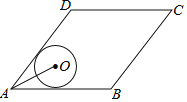
【題目】如圖,菱形ABCD的邊AB=5,面積為20,∠BAD<90°,⊙O與邊AB、AD都相切,AO=2,則⊙O的半徑長(zhǎng)等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】投資1萬(wàn)元圍一個(gè)矩形菜園(如圖),其中一邊靠墻,另外三邊選用不同材料建造.墻長(zhǎng)24 m,平行于墻的邊的費(fèi)用為200元/m,垂直于墻的邊的費(fèi)用為150元/m,設(shè)平行于墻的邊長(zhǎng)為x m.
(1)設(shè)垂直于墻的一邊長(zhǎng)為y m,直接寫(xiě)出y與x之間的函數(shù)關(guān)系式;
(2)若菜園面積為384 m2,求x的值;
(3)求菜園的最大面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在ABCD中,E、F分別為邊AD、BC的中點(diǎn),對(duì)角線(xiàn)AC分別交BE,DF于點(diǎn)G、H.求證:AG=CH.
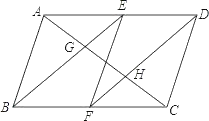
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校根據(jù)課程設(shè)置要求,開(kāi)設(shè)了數(shù)學(xué)類(lèi)拓展性課程,為了解學(xué)生最喜歡的課程內(nèi)容,隨機(jī)抽取了部分學(xué)生進(jìn)行問(wèn)卷調(diào)查(每人必須且只選中其中一項(xiàng)),并將統(tǒng)計(jì)結(jié)果繪制成如下統(tǒng)計(jì)圖(不完整),請(qǐng)根據(jù)圖中信息回答問(wèn)題:
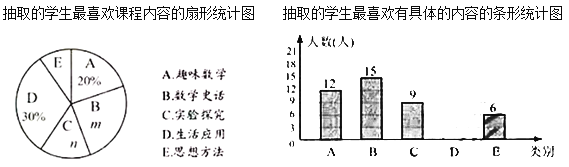
(1)求m,n的值.
(2)補(bǔ)全條形統(tǒng)計(jì)圖.
(3)該校共有1200名學(xué)生,試估計(jì)全校最喜歡“數(shù)學(xué)史話(huà)”的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=BC=3cm.動(dòng)點(diǎn)P從點(diǎn)A出發(fā),以![]() cm/s的速度沿AB方向運(yùn)動(dòng)到點(diǎn)B.動(dòng)點(diǎn)Q同時(shí)從點(diǎn)A出發(fā),以1cm/s的速度沿折線(xiàn)AC
cm/s的速度沿AB方向運(yùn)動(dòng)到點(diǎn)B.動(dòng)點(diǎn)Q同時(shí)從點(diǎn)A出發(fā),以1cm/s的速度沿折線(xiàn)AC![]() CB方向運(yùn)動(dòng)到點(diǎn)B.設(shè)△APQ的面積為y(cm2).運(yùn)動(dòng)時(shí)間為x(s),則下列圖象能反映y與x之間關(guān)系的是 ( )
CB方向運(yùn)動(dòng)到點(diǎn)B.設(shè)△APQ的面積為y(cm2).運(yùn)動(dòng)時(shí)間為x(s),則下列圖象能反映y與x之間關(guān)系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】數(shù)學(xué)課上,潘老師給出如下定義:如果一個(gè)三角形有一邊上的高線(xiàn)等于這條邊的一半,那么稱(chēng)這個(gè)三角形為“垂美三角形”,這條邊稱(chēng)為這個(gè)三角形的“垂美邊”.
概念理解:
(1)如圖①,已知∠A=90°,AB=AC,請(qǐng)證明等腰Rt△ABC一定是“垂美三角形”.
探索運(yùn)用:
(2)已知等腰△ABC是“垂美三角形”,請(qǐng)求出頂角的度數(shù).
能力提升:
(3)如圖②,在直角坐標(biāo)系中,點(diǎn)A為x軸正半軸上動(dòng)點(diǎn),在反比例函數(shù)![]() 的圖象上是否存在點(diǎn)B,使△OAB是“垂美三角形”,且OA,OB均為“垂美邊”,若存在,請(qǐng)求出點(diǎn)B的坐標(biāo).
的圖象上是否存在點(diǎn)B,使△OAB是“垂美三角形”,且OA,OB均為“垂美邊”,若存在,請(qǐng)求出點(diǎn)B的坐標(biāo).
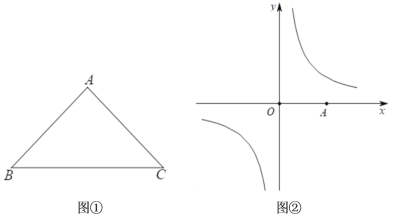
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】大學(xué)生自主創(chuàng)業(yè),集資5萬(wàn)元開(kāi)品牌專(zhuān)賣(mài)店,已知該品牌商品成本為每件a元,市場(chǎng)調(diào)查發(fā)現(xiàn)日銷(xiāo)售量y(件)與銷(xiāo)售價(jià)x(元/件)之間存在一次函數(shù)關(guān)系如表:
銷(xiāo)售價(jià)x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
銷(xiāo)售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若該店某天的銷(xiāo)售價(jià)定為110元/件,雇有3名員工,則當(dāng)天正好收支平衡(其中支出=商品成本+員工工資+應(yīng)支付其它費(fèi)用):已知員工的工資為每人每天100元,每天還應(yīng)支付其它費(fèi)用為200元(不包括集資款).
(1)求日銷(xiāo)售量y(件)與銷(xiāo)售價(jià)x(元/件)之間的函數(shù)關(guān)系式;
(2)該店現(xiàn)有2名員工,試求每件服裝的銷(xiāo)售價(jià)定為多少元時(shí),該服裝店每天的毛利潤(rùn)最大:(毛利潤(rùn)═銷(xiāo)售收入一商品成本一員工工資一應(yīng)支付其他費(fèi)用)
(3)在(2)的條件下,若每天毛利潤(rùn)全部積累用于一次性還款,而集資款每天應(yīng)按其萬(wàn)分之二的利率支付利息,則該店最少需要多少天(取整數(shù))才能還清集資款?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com