
【題目】如圖,在△ABC中,∠C=90°,AC=BC=3cm.動點P從點A出發,以![]() cm/s的速度沿AB方向運動到點B.動點Q同時從點A出發,以1cm/s的速度沿折線AC
cm/s的速度沿AB方向運動到點B.動點Q同時從點A出發,以1cm/s的速度沿折線AC![]() CB方向運動到點B.設△APQ的面積為y(cm2).運動時間為x(s),則下列圖象能反映y與x之間關系的是 ( )
CB方向運動到點B.設△APQ的面積為y(cm2).運動時間為x(s),則下列圖象能反映y與x之間關系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
【答案】D
【解析】
在△ABC中,∠C=90°,AC=BC=3cm,可得AB=![]() ,∠A=∠B=45°,分當0<x≤3(點Q在AC上運動,點P在AB上運動)和當3≤x≤6時(點P與點B重合,點Q在CB上運動)兩種情況求出y與x的函數關系式,再結合圖象即可解答.
,∠A=∠B=45°,分當0<x≤3(點Q在AC上運動,點P在AB上運動)和當3≤x≤6時(點P與點B重合,點Q在CB上運動)兩種情況求出y與x的函數關系式,再結合圖象即可解答.
在△ABC中,∠C=90°,AC=BC=3cm,可得AB=![]() ,∠A=∠B=45°,當0<x≤3時,點Q在AC上運動,點P在AB上運動(如圖1), 由題意可得AP=
,∠A=∠B=45°,當0<x≤3時,點Q在AC上運動,點P在AB上運動(如圖1), 由題意可得AP=![]() x,AQ=x,過點Q作QN⊥AB于點N,在等腰直角三角形AQN中,求得QN=
x,AQ=x,過點Q作QN⊥AB于點N,在等腰直角三角形AQN中,求得QN=![]() x,所以y=
x,所以y=![]() =
=![]() (0<x≤3),即當0<x≤3時,y隨x的變化關系是二次函數關系,且當x=3時,y=4.5;當3≤x≤6時,點P與點B重合,點Q在CB上運動(如圖2),由題意可得PQ=6-x,AP=3
(0<x≤3),即當0<x≤3時,y隨x的變化關系是二次函數關系,且當x=3時,y=4.5;當3≤x≤6時,點P與點B重合,點Q在CB上運動(如圖2),由題意可得PQ=6-x,AP=3![]() ,過點Q作QN⊥BC于點N,在等腰直角三角形PQN中,求得QN=
,過點Q作QN⊥BC于點N,在等腰直角三角形PQN中,求得QN=![]() (6-x),所以y=
(6-x),所以y=![]() =
=![]() (3≤x≤6),即當3≤x≤6時,y隨x的變化關系是一次函數,且當x=6時,y=0.由此可得,只有選項D符合要求,故選D.
(3≤x≤6),即當3≤x≤6時,y隨x的變化關系是一次函數,且當x=6時,y=0.由此可得,只有選項D符合要求,故選D.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
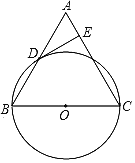
【題目】已知:如圖,在△ABC中,BC=AC,以BC為直徑的⊙O與邊AB相交于點D,DE⊥AC,垂足為點E.
(1)求證:點D是AB的中點;
(2)判斷DE與⊙O的位置關系,并證明你的結論;
(3)若⊙O的直徑為10,tanB=3,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場以每件10元的價格購進一種商品,試銷中發現,這種商品每天的銷售量m(件)與每件的銷售價x(元)滿足一次函數,其函數圖像如圖所示.

(1)求商場每天銷售這種商品的銷售利潤y(元)與每件的銷售價x(元)之間的函數解析式;
(2)試判斷,每件商品的銷售價格在什么范圍內,每天的銷售利潤隨著價格的提高而增加.
查看答案和解析>>
科目:初中數學 來源: 題型:
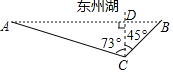
【題目】某市為了創建綠色生態城市,在城東建了“東州湖”景區,小明和小亮想測量“東州湖”東西兩端A、B間的距離.于是,他們去了湖邊,如圖,在湖的南岸的水平地面上,選取了可直接到達點B的一點C,并測得BC=350米,點A位于點C的北偏西73°方向,點B位于點C的北偏東45°方向.請你根據以上提供的信息,計算“東州湖”東西兩端之間AB的長.(結果精確到1米)(參考數據:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
科目:初中數學 來源: 題型:
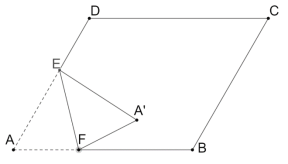
【題目】如圖,在菱形![]() 中,
中,![]() ,
, ![]() , 點
, 點![]() 在邊
在邊![]() 上,且
上,且![]() ,點
,點![]() 為線段
為線段![]() 上一動點(不與點
上一動點(不與點![]() 重合),將菱形沿直線
重合),將菱形沿直線![]() 折疊,點
折疊,點![]() 的對應點為點
的對應點為點![]() ,當
,當![]() 落在菱形的對角線上時,
落在菱形的對角線上時,![]() 的長為__________.
的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
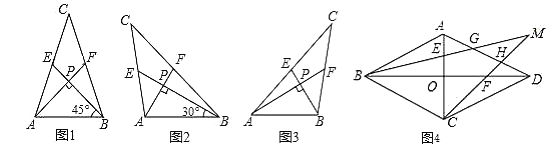
【題目】我們把兩條中線互相垂直的三角形稱為“中垂三角形”.例如圖1,圖2,圖3中,![]() ,
,![]() 是
是![]() 的中線,
的中線,![]() ,垂足為
,垂足為![]() .像
.像![]() 這樣的三角形均為“中垂三角形”.設
這樣的三角形均為“中垂三角形”.設![]() ,
,![]() ,
,![]() .
.
特例探索:
(1)①如圖1,當![]() ,
,![]() 時,
時,![]() _________,
_________,![]() ________;
________;
②如圖2,當![]() ,
,![]() 時,求
時,求![]() 和
和![]() 的值.
的值.
歸納證明:
(2)請你觀察(1)中的計算結果,猜想三者之間的關系,用等式表示出來,并利用圖3證明你發現的關系式.
(3)利用(2)中的結論,解答下列問題:在邊長為3的菱形![]() 中,
中,![]() 為對角線
為對角線![]() ,
,![]() 的交點,
的交點,![]() 分別為線段
分別為線段![]() ,
,![]() 的中點,連接
的中點,連接![]() ,
,![]() 并延長交于點
并延長交于點![]() ,
,![]() ,
,![]() 分別交
分別交![]() 于點
于點![]() ,
,![]() ,如圖4所示,求
,如圖4所示,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
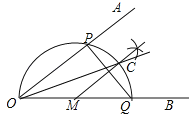
【題目】已知∠AOB,作圖.
步驟1:在OB上任取一點M,以點M為圓心,MO長為半徑畫半圓,分別交OA、OB于點P、Q;
步驟2:過點M作PQ的垂線交 ![]() 于點C;
于點C;
步驟3:畫射線OC.
則下列判斷:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正確的個數為( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正確的個數為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩種糖果,原價分別為每千克a元和b元.根據調查,將兩種糖果按甲種糖果x千克與乙種糖果y千克的比例混合,取得了較好的銷售效果.現在糖果價格有了調整:甲種糖果單價下降15%,乙種糖果單價上漲20%,但按原比例混合的糖果單價恰好不變,則![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com